කොන් හතරකට වඩා ඇති වඩාත් ප්‍රසිද්ධ රූපය සාමාන්‍ය ෂඩාස්‍රයයි. ජ්යාමිතිය තුළ, එය බොහෝ විට ගැටළු වලදී භාවිතා වේ. ජීවිතයේ දී, කප්පාදුව මත පැණි වදන් ඇත්තේ මෙයයි.
එය වැරදියට වඩා වෙනස් වන්නේ කෙසේද?
පළමුව, ෂඩාස්‍රය යනු සිරස් 6ක් සහිත රූපයකි. දෙවනුව, එය උත්තල හෝ අවතල විය හැක. පළමු එක වෙනස් වන්නේ අනෙක් දෙක හරහා ඇද ගන්නා ලද සරල රේඛාවක එක් පැත්තක සිරස් හතරක් පිහිටා තිබීමයි.
තෙවනුව, නිත්ය ෂඩාස්‍රය එහි සියලුම පැති සමාන බව මගින් සංලක්ෂිත වේ. එපමණක්ද නොව, රූපයේ සෑම කොනකටම එකම අගයක් ඇත. එහි සියලුම කෝණවල එකතුව තීරණය කිරීම සඳහා, ඔබට සූත්‍රය භාවිතා කිරීමට අවශ්ය වනු ඇත: 180º * (n - 2). මෙහි n යනු රූපයේ සිරස් ගණනයි, එනම් 6. සරල ගණනය කිරීමකින් 720º අගයක් ලැබේ. එබැවින් සෑම කෝණයක්ම අංශක 120 කි.
එදිනෙදා කටයුතුවලදී, හිම පියල්ලක් සහ ගෙඩියක් තුළ නිත්ය ෂඩාස්රයක් දක්නට ලැබේ. රසායනඥයින් බෙන්සීන් අණුව තුළ පවා එය දකියි.
ගැටළු විසඳීමේදී ඔබ දැනගත යුතු ගුණාංග මොනවාද?
ඉහත දක්වා ඇති දේට එකතු කළ යුතුය:
- කේන්ද්‍රය හරහා ඇද ගන්නා ලද රූපයේ විකර්ණ, එය සමපාර්ශ්වික වන ත්රිකෝණ හයකට බෙදේ;
- නිත්ය ෂඩාස්රයක පැත්තේ අගයක් ඇති අතර එය වටා ඇති කවයේ අරය සමඟ සමපාත වේ;
- එවැනි රූපයක් භාවිතා කිරීමෙන්, තලය පිරවිය හැකි අතර, ඒවා අතර හිඩැස් සහ අතිච්ඡාදනය සිදු නොවේ.
හඳුන්වා දුන් අංකනය
සාම්ප්‍රදායිකව, සාමාන්‍ය ජ්‍යාමිතික රූපයක පැත්ත ලතින් අකුර "a" මගින් දැක්වේ. ගැටළු විසඳීම සඳහා, ප්රදේශය සහ පරිමිතිය ද අවශ්ය වේ, මේවා පිළිවෙලින් S සහ P වේ. කවයක් සාමාන්‍ය ෂඩාස්රයක කොටා ඇත හෝ ඒ වටා වට කර ඇත. එවිට ඒවායේ අරය සඳහා අගයන් ඇතුළත් වේ. ඒවා පිළිවෙලින් r සහ R අක්ෂර වලින් දැක්වේ.
සමහර සූත්‍රවල, අභ්‍යන්තර කෝණයක්, අර්ධ පරිමිතියක් සහ අපොතම් (බහුඅස්‍රයේ කේන්ද්‍රයේ සිට ඕනෑම පැත්තක මැදට ලම්බක වන) දිස්වේ. ඔවුන් සඳහා අකුරු භාවිතා වේ: α, p, m.
රූපයක් විස්තර කරන සූත්‍ර
ලියා ඇති කවයක අරය ගණනය කිරීම සඳහා, ඔබට මෙය අවශ්ය වේ: r= (a * √3) / 2, සහ r = m. එනම් එම සූත්‍රය අපෝත්තමය සඳහා වනු ඇත.
ෂඩාස්රයක පරිමිතිය සියලු පැතිවල එකතුව වන බැවින්, එය පහත පරිදි තීරණය කරනු ලැබේ: P = 6 * a. පැත්ත වටකුරු රවුමේ අරයට සමාන බැවින්, පරිමිතිය සඳහා සාමාන්‍ය ෂඩාස්රයක් සඳහා එවැනි සූත්‍රයක් තිබේ: P \u003d 6 * R. සෙල්ලිපි කළ කවයේ අරය සඳහා ලබා දී ඇති එකෙන්, a අතර සම්බන්ධතාවය සහ r ව්‍යුත්පන්න වේ. එවිට සූත්‍රය පහත ස්වරූපය ගනී: Р = 4 r * √3.
සාමාන්‍ය ෂඩාස්රයක ප්රදේශය සඳහා, මෙය ප්‍රයෝජනවත් විය හැකිය: S = p * r = (a 2 * 3 √3) / 2.
කාර්යයන්
අංක 1. කොන්දේසිය.නිත්ය ෂඩාස්‍ර ප්‍රිස්මයක් ඇත, එහි එක් එක් දාරය සෙන්ටිමීටර 4 ට සමාන වේ.එහි සිලින්ඩරයක් සටහන් කර ඇති අතර එහි පරිමාව තීරණය කළ යුතුය.
විසඳුමක්.සිලින්ඩරයක පරිමාව නිර්වචනය කරනු ලබන්නේ පාදයේ ප්රදේශයේ සහ උසෙහි නිෂ්පාදනයක් ලෙසය. දෙවැන්න ප්රිස්මයේ මායිම සමග සමපාත වේ. තවද එය සාමාන්‍ය ෂඩාස්රයක පැත්තට සමාන වේ. එනම්, සිලින්ඩරයේ උස ද 4 සෙ.මී.
එහි පාදයේ ප්රදේශය සොයා ගැනීමට, ඔබ ෂඩාස්‍රයේ කොටා ඇති රවුමේ අරය ගණනය කළ යුතුය. මේ සඳහා වන සූත්‍රය ඉහත පෙන්වා ඇත. එබැවින් r = 2√3 (cm). එවිට රවුමේ ප්රදේශය: S \u003d π * r 2 \u003d 3.14 * (2√3) 2 \u003d 37.68 (cm 2).
පිළිතුර. V \u003d 150.72 cm 3.
අංක 2. කොන්දේසිය.සාමාන්‍ය ෂඩාස්රයක කොටා ඇති කවයක අරය ගණනය කරන්න. එහි පැත්ත √3 සෙ.මී., එහි පරිමිතිය කුමක් වේද?
විසඳුමක්.මෙම කාර්යය සඳහා ඉහත සූත්‍ර දෙකක් භාවිතා කිරීම අවශ්ය වේ. එපමණක්ද නොව, ඒවා වෙනස් කිරීමකින් තොරව යෙදිය යුතුය, පැත්තේ අගය ආදේශ කර ගණනය කරන්න.
මේ අනුව, ශිලාලේඛන රවුමේ අරය 1.5 සෙ.මී. පරිමිතිය සඳහා පහත අගය නිවැරදි වේ: 6√3 සෙ.මී.
පිළිතුර. r = 1.5 cm, Р = 6√3 cm.
අංක 3. කොන්දේසිය.වටකුරු රවුමේ අරය 6 සෙ.මී. සාමාන්‍ය ෂඩාස්රයක පැත්තේ අගය කුමක්ද?
විසඳුමක්.ෂඩාස්රයක කොටා ඇති කවයක අරය සඳහා වන සූත්‍රයෙන්, පැත්ත ගණනය කළ යුතු එක කෙනෙකුට පහසුවෙන් ලබා ගත හැක. අරය දෙකකින් ගුණ කර තුනේ මුලින් බෙදන බව පැහැදිලිය. හරය තුළ ඇති අහේතුක බව නැති කිරීම අවශ්‍යයි. එබැවින්, ක්රියාවන්ගේ ප්රතිඵලය පහත දැක්වෙන ආකාරය ගනී: (12 √3) / (√3 * √3), එනම් 4√3.
පිළිතුර. a = 4√3 සෙ.මී.
සාමාන්‍ය ෂඩාස්රයක පෙනුම කෙබඳුදැයි ඔබ දන්නවාද?
මේ ප්‍රශ්නය අහම්බෙන් අහපු එකක් නෙවෙයි. 11 ශ්‍රේණියේ බොහෝ සිසුන් එයට පිළිතුර නොදනී.
නිත්ය ෂඩාස්රයක් යනු සියලු පැති සමාන වන අතර සියලු කෝණ ද සමාන වේ..
යකඩ ගෙඩිය. හිම පියලි. මී මැස්සන් ජීවත් වන පැණි වද සෛලයකි. බෙන්සීන් අණුව. මෙම වස්තූන්ට පොදු වන්නේ කුමක්ද? - ඔවුන් සියල්ලන්ටම නිතිපතා ෂඩාස්රාකාර හැඩයක් තිබීම.
සාමාන්‍ය ෂඩාස්‍රය සඳහා කාර්යයන් දකින විට බොහෝ පාසල් සිසුන් අහිමි වන අතර ඒවා විසඳීමට විශේෂ සූත්‍ර කිහිපයක් අවශ්ය බව ඔවුහු විශ්වාස කරති. ඒක එහෙමද?
සාමාන්‍ය ෂඩාස්රයක විකර්ණ අඳින්න. අපට සමපාර්ශ්වික ත්රිකෝණ හයක් ලැබුණා. 
සමපාර්ශ්වික ත්රිකෝණයක ප්රදේශය බව අපි දනිමු.
එවිට නිත්ය ෂඩාස්රයක ප්රදේශය හය ගුණයකින් විශාල වේ.
සාමාන්‍ය ෂඩාස්රයක පැත්ත කොහෙද.
සාමාන්‍ය ෂඩාස්රයක, එහි මධ්‍යයේ සිට ඕනෑම ශීර්ෂයකට ඇති දුර සමාන වන අතර සාමාන්‍ය ෂඩාස්‍රයේ පැත්තට සමාන බව කරුණාවෙන් සලකන්න.
මෙයින් අදහස් කරන්නේ නිත්ය ෂඩාස්රයක් වටා ඇති වෘත්තයක අරය එහි පැත්තට සමාන බවයි.
සාමාන්‍ය ෂඩාස්රයක කොටා ඇති කවයක අරය සොයා ගැනීම පහසුය.
ඔහු සමාන ය.
දැන් ඔබට සාමාන්‍ය ෂඩාස්රයක් දිස්වන ඕනෑම භාවිත ගැටළු පහසුවෙන් විසඳාගත හැක.
පැත්තක් සහිත නිත්ය ෂඩාස්රයක කොටා ඇති කවයක අරය සොයන්න.
එවැනි වෘත්තයක අරය වේ.
පිළිතුර: .
6 ක අරයක් සහිත රවුමක කොටා ඇති සාමාන්‍ය ෂඩාස්රයක පැත්ත කුමක්ද?
සාමාන්‍ය ෂඩාස්රයක පැත්ත එය වටා ඇති රවුමේ අරයට සමාන බව අපි දනිමු.
සාමාන්‍ය ෂඩාස්රයක පෙනුම කෙබඳුදැයි ඔබ දන්නවාද?
මේ ප්‍රශ්නය අහම්බෙන් අහපු එකක් නෙවෙයි. 11 ශ්‍රේණියේ බොහෝ සිසුන් එයට පිළිතුර නොදනී.
නිත්ය ෂඩාස්රයක් යනු සියලු පැති සමාන වන අතර සියලු කෝණ ද සමාන වේ..
යකඩ ගෙඩිය. හිම පියලි. මී මැස්සන් ජීවත් වන පැණි වද සෛලයකි. බෙන්සීන් අණුව. මෙම වස්තූන්ට පොදු වන්නේ කුමක්ද? - ඔවුන් සියල්ලන්ටම නිතිපතා ෂඩාස්රාකාර හැඩයක් තිබීම.
සාමාන්‍ය ෂඩාස්‍රය සඳහා කාර්යයන් දකින විට බොහෝ පාසල් සිසුන් අහිමි වන අතර ඒවා විසඳීමට විශේෂ සූත්‍ර කිහිපයක් අවශ්ය බව ඔවුහු විශ්වාස කරති. ඒක එහෙමද?
සාමාන්‍ය ෂඩාස්රයක විකර්ණ අඳින්න. අපට සමපාර්ශ්වික ත්රිකෝණ හයක් ලැබුණා.
සමපාර්ශ්වික ත්රිකෝණයක ප්රදේශය බව අපි දනිමු.
එවිට නිත්ය ෂඩාස්රයක ප්රදේශය හය ගුණයකින් විශාල වේ.
සාමාන්‍ය ෂඩාස්රයක පැත්ත කොහෙද.
සාමාන්‍ය ෂඩාස්රයක, එහි මධ්‍යයේ සිට ඕනෑම ශීර්ෂයකට ඇති දුර සමාන වන අතර සාමාන්‍ය ෂඩාස්‍රයේ පැත්තට සමාන බව කරුණාවෙන් සලකන්න.
මෙයින් අදහස් කරන්නේ නිත්ය ෂඩාස්රයක් වටා ඇති වෘත්තයක අරය එහි පැත්තට සමාන බවයි.
සාමාන්‍ය ෂඩාස්රයක කොටා ඇති කවයක අරය සොයා ගැනීම පහසුය.
ඔහු සමාන ය.
දැන් ඔබට සාමාන්‍ය ෂඩාස්රයක් දිස්වන ඕනෑම භාවිත ගැටළු පහසුවෙන් විසඳාගත හැක.
පැත්තක් සහිත නිත්ය ෂඩාස්රයක කොටා ඇති කවයක අරය සොයන්න.
එවැනි වෘත්තයක අරය වේ.
පිළිතුර: .
6 ක අරයක් සහිත රවුමක කොටා ඇති සාමාන්‍ය ෂඩාස්රයක පැත්ත කුමක්ද?
සාමාන්‍ය ෂඩාස්රයක පැත්ත එය වටා ඇති රවුමේ අරයට සමාන බව අපි දනිමු.
රවුමක කොටා ඇති නිත්ය ෂඩාස්රයක් තැනීම.ෂඩාස්රාකාර ඉදිකිරීම පදනම් වන්නේ එහි පැත්ත වටකුරු රවුමේ අරයට සමාන වන බැවිනි. එබැවින්, ගොඩ නැගීම සඳහා, රවුම සමාන කොටස් හයකට බෙදීමට සහ සොයාගත් කරුණු එකිනෙකට සම්බන්ධ කිරීම ප්රමාණවත් වේ (රූපය 60, a).
T-square සහ 30X60° වර්ග භාවිතා කරමින් නිත්ය ෂඩාස්රයක් සෑදිය හැක. මෙම ඉදිකිරීම සිදු කිරීම සඳහා, අපි රවුමේ තිරස් විෂ්කම්භය කෝණ 1 සහ 4 (පය. 60, ආ) ද්වි අංශය ලෙස ගනිමු, පැති 1-6, 4-3, 4-5 සහ 7-2 ගොඩනඟමු, ඉන්පසු අපි පැති 5-6 සහ 3-2 අඳින්න.
රවුමක කොටා ඇති සමපාර්ශ්වික ත්රිකෝණයක් තැනීම. එවැනි ත්රිකෝණයක සිරස් මාලිමා යන්ත්රයක් සහ 30 සහ 60 of කෝණ සහිත චතුරස්රයක් හෝ එක් මාලිමාවක් පමණක් භාවිතයෙන් ගොඩනගා ගත හැකිය.
රවුමක කොටා ඇති සමපාර්ශ්වික ත්රිකෝණයක් තැනීමට ක්‍රම දෙකක් සලකා බලන්න.
පළමු මාර්ගය(රූපය 61, a) පදනම් වන්නේ ත්රිකෝණයේ 7, 2, 3 කෝණ තුනම 60 ° බැගින් අඩංගු වන අතර, 7 වන ලක්ෂ්‍යය හරහා අඳින ලද සිරස් රේඛාව කෝණය 1 හි උස සහ ද්වි අංශය යන දෙකම වේ. කෝණය 0-1- 2 30 ° ට සමාන වේ, පසුව පැත්ත සොයා ගැනීමට
1-2, එය 1 වන ස්ථානයේ සහ 0-1 පැත්තේ 30 ° ක කෝණයක් ගොඩනැගීමට ප්රමාණවත් වේ. මෙය සිදු කිරීම සඳහා, රූපයේ දැක්වෙන පරිදි ටී-චතුරස්රය සහ හතරැස් සකසන්න, 1-2 රේඛාවක් අඳින්න, එය අපේක්ෂිත ත්රිකෝණයේ පැතිවලින් එකක් වනු ඇත. 2-3 පැත්ත ගොඩනැගීමට, ඉරි සහිත රේඛා මගින් පෙන්වන ස්ථානයට T-චතුරශ්‍රය සකසා, 2 වන ලක්ෂ්‍යය හරහා සරල රේඛාවක් අඳින්න, එය ත්රිකෝණයේ තුන්වන ශීර්ෂය නිර්වචනය කරයි.
දෙවන මාර්ගයඔබ රවුමක කොටා ඇති සාමාන්‍ය ෂඩාස්රයක් ගොඩනඟා එහි සිරස් එකක් හරහා සම්බන්ධ කළහොත් ඔබට සමපාර්ශ්වික ත්රිකෝණයක් ලැබේ යන කාරණය මත පදනම් වේ.
ත්රිකෝණයක් ඉදි කිරීම සඳහා (රූපය 61, b), අපි විෂ්කම්භය මත ශීර්ෂ-ලක්ෂ්ය 1 සලකුණු කර 1-4 විෂ්කම්භය සහිත රේඛාවක් අඳින්නෙමු. තවද, D / 2 ට සමාන අරයක් සහිත 4 වන ලක්ෂයේ සිට, 3 සහ 2 යන ස්ථානවල රවුම සමඟ ඡේදනය වන තෙක් අපි චාපය විස්තර කරමු. ප්රතිඵලය වන ලක්ෂ්ය අපේක්ෂිත ත්රිකෝණයේ තවත් සිරස් දෙකක් වනු ඇත.
රවුමක කොටා ඇති චතුරස්රයක් ඉදිකිරීම. මෙම ඉදිකිරීම චතුරස්රයක් සහ මාලිමාවක් භාවිතයෙන් සිදු කළ හැකිය.
පළමු ක්‍රමය පදනම් වන්නේ චතුරස්රයේ විකර්ණ වටකුරු රවුමේ මධ්‍යයේ ඡේදනය වන අතර 45 ° ක කෝණයකින් එහි අක්ෂවලට නැඹුරු වීමයි. මේ මත පදනම්ව, අපි රූපයේ දැක්වෙන පරිදි ටී-චතුරස්රයක් සහ 45 ° කෝණ සහිත චතුරස්රයක් ස්ථාපනය කරමු. 62, a, සහ ලකුණු 1 සහ 3 ලකුණු කරන්න. තව දුරටත්, මෙම ලක්ෂ්ය හරහා, අපි T-square ආධාරයෙන් 4-1 සහ 3-2 වර්ග වල තිරස් පැති අඳින්නෙමු. ඉන්පසුව, චතුරස්රයේ කකුල දිගේ T-square භාවිතා කරමින්, අපි වර්ග 1-2 සහ 4-3 හි සිරස් පැති අඳින්නෙමු.
දෙවන ක්‍රමය පදනම් වන්නේ චතුරස්රයේ සිරස් විෂ්කම්භයේ කෙළවර අතර වසා ඇති රවුමේ චාප දෙකට බෙදීම මත ය (රූපය 62, ආ). අපි අන්‍යෝන්‍ය වශයෙන් ලම්බක විෂ්කම්භයන් දෙකක කෙළවරේ A, B සහ C ලකුණු සලකුණු කරන අතර, ඒවායින් y අරය සමඟ අපි චාප ඡේදනය වන තෙක් විස්තර කරමු.
තවද, චාප ඡේදනය වන ස්ථාන හරහා, අපි ඝන රේඛා සමඟ රූපයේ සලකුණු කර ඇති සහායක රේඛා අඳින්නෙමු. රවුම සමඟ ඔවුන්ගේ ඡේදනය වීමේ ලක්ෂ්ය 1 සහ 3 සිරස් නිර්වචනය කරනු ඇත. 4 සහ 2. මේ ආකාරයෙන් ලබාගත් අපේක්ෂිත චතුරස්රයේ සිරස් එකිනෙක සම්බන්ධ වේ.
රවුමක කොටා ඇති සාමාන්‍ය පෙන්ටගනයක් තැනීම.
රවුමක නිතිපතා පෙන්ටගනයක් සටහන් කිරීම සඳහා (රූපය 63), අපි පහත සඳහන් ඉදිකිරීම් සිදු කරමු.
අපි රවුමේ 1 ලක්ෂය සලකුණු කර එය පෙන්ටගනයේ සිරස් වලින් එකක් ලෙස ගනිමු. AO කොටස අඩකින් බෙදන්න. මෙය සිදු කිරීම සඳහා, A ලක්ෂ්‍යයේ සිට AO අරය සමඟ, අපි M සහ B ලක්ෂ්‍යවල රවුම සමඟ ඡේදනය දක්වා චාපය විස්තර කරමු. මෙම ලක්ෂ්ය සරල රේඛාවක් සමඟ සම්බන්ධ කිරීමෙන්, අපි ලක්ෂ්‍යය K ලබා ගනිමු, එය අපි 1 ලක්ෂයට සම්බන්ධ කරමු. A7 ඛණ්ඩයට සමාන අරයක් සහිතව, අපි K ලක්ෂ්‍යයේ සිට ඡේදනය වන චාපය AO ලක්ෂ්‍යයේ විෂ්කම්භක රේඛාව සමඟ ඡේදනය දක්වා විස්තර කරමු. ලක්ෂ්‍යය 1 H ලක්ෂ්‍යය සමඟ සම්බන්ධ කිරීමෙන්, අපට පෙන්ටගනයේ පැත්ත ලැබේ. ඉන්පසුව, 1H කොටසට සමාන මාලිමා විවරයක් සමඟ, 1 වන ශීර්ෂයේ සිට රවුම සමඟ ඡේදනය දක්වා චාපය විස්තර කරමින්, අපට සිරස් 2 සහ 5 හමු වේ. එම මාලිමා විවරය සමඟම 2 සහ 5 සිරස් වලින් සටහන් කර, ඉතිරි කොටස අපි ලබා ගනිමු. සිරස් 3 සහ 4. අපි සොයාගත් කරුණු එකිනෙකට අනුපිළිවෙලින් සම්බන්ධ කරමු.
එහි පැත්ත ලබා දී ඇති නිත්ය පෙන්ටගනයක් තැනීම.
එහි දී ඇති පැත්ත දිගේ නිතිපතා පෙන්ටගනයක් තැනීම සඳහා (රූපය 64), අපි AB කොටස සමාන කොටස් හයකට බෙදන්නෙමු. AB අරය සහිත A සහ B ලක්ෂ්ය වලින් අපි චාප විස්තර කරමු, එහි ඡේදනය K ලක්ෂ්‍යය ලබා දෙනු ඇත. මෙම ලක්ෂ්‍යය සහ AB රේඛාවේ 3 වන බෙදීම හරහා අපි සිරස් රේඛාවක් අඳින්නෙමු.
අපි පෙන්ටගනයේ 1-ශීර්ෂය ලබා ගනිමු. ඉන්පසුව, AB ට සමාන අරයක් සහිතව, 1 ලක්ෂයේ සිට අපි චාපය ඡේදනය දක්වා විස්තර කරමු A සහ B ලක්ෂ්ය වලින් කලින් අඳින ලද චාප සමඟ. චාපවල ඡේදනය වන ස්ථාන පෙන්ටගනයේ 2 සහ 5 හි සිරස් තීරණය කරයි. අපි සොයාගත් දේ සම්බන්ධ කරමු. එකිනෙකා සමඟ ශ්‍රේණියේ සිරස්.
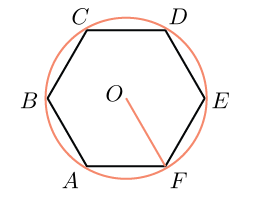
රවුමක කොටා ඇති නිත්ය සප්තකෝෂයක් තැනීම.
විෂ්කම්භය D කවයක් ලබා දෙන්න; ඔබ එයට සාමාන්‍ය හෙප්ටගනයක් සටහන් කළ යුතුය (රූපය 65). රවුමේ සිරස් විෂ්කම්භය සමාන කොටස් හතකට බෙදන්න. D කවයේ විෂ්කම්භයට සමාන අරයක් සහිත 7 වන ස්ථානයේ සිට, F ලක්ෂ්‍යයේ තිරස් විෂ්කම්භය අඛණ්ඩව ඡේදනය වන තෙක් අපි චාපය විස්තර කරමු. VII ලක්ෂ්‍යය හෙප්ටගනයේ සිරස් වලින් එකක් ලෙස ගෙන, අපි සිරස් විෂ්කම්භයේ ඒකාකාර බෙදීම් හරහා F ධ්‍රැවයේ සිට කිරණ අඳින්නෙමු, රවුම සමඟ ඡේදනය වීම හෙප්ටගනයේ VI, V සහ IV ශීර්ෂයන් තීරණය කරයි. IV, V සහ VI ලක්ෂ්ය වලින් සිරස් / - // - /// ලබා ගැනීම සඳහා, අපි ඒවා රවුම සමඟ ඡේදනය වන තෙක් තිරස් රේඛා අඳින්නෙමු. අපි එකිනෙකා සමඟ ශ්රේණිගතව සොයාගත් සිරස් සම්බන්ධ කරමු. F ධ්‍රැවයේ සිට සහ සිරස් විෂ්කම්භයේ ඔත්තේ බෙදීම් හරහා කිරණ ඇඳීමෙන් හෙප්ටගනය ගොඩනැගිය හැක.
ඉහත ක්‍රමය ඕනෑම පැති ගණනක් සහිත නිත්ය බහුඅස්‍ර තැනීම සඳහා සුදුසු වේ.
රවුම ඕනෑම සමාන කොටස් ගණනකට බෙදීම වගුවේ ඇති දත්ත භාවිතයෙන්ද සිදු කළ හැක. 2, නිත්ය ශිලා ලේඛනගත බහුඅස්‍රවල පැතිවල මානයන් තීරණය කිරීමට හැකි වන සංගුණක පෙන්වයි.
පාසල් විෂය මාලාවේ බහුඅස්‍ර යන මාතෘකාව ආවරණය වී ඇතත් ඔවුන් ඒ ගැන ප්රමාණවත් අවධානයක් යොමු නොකරයි. මේ අතර, එය සිත්ගන්නාසුළු වන අතර මෙය සාමාන්‍ය ෂඩාස්‍රය හෝ ෂඩාස්‍රය සම්බන්ධයෙන් විශේෂයෙන් සත්‍ය වේ - සියල්ලට පසු, බොහෝ ස්වාභාවික වස්තූන් මෙම හැඩය ඇත. මේවාට පැණි වද සහ තවත් දේ ඇතුළත් වේ. මෙම පෝරමය ප්රායෝගිකව ඉතා හොඳින් අදාළ වේ.
නිර්වචනය සහ ඉදිකිරීම්
සාමාන්‍ය ෂඩාස්‍රය යනු දිගට සමාන පැති හයක් සහ සමාන කෝණ සංඛ්‍යාවක් ඇති තල රූපයකි.
අපි බහුඅස්‍රයක කෝණවල එකතුව සඳහා සූත්‍රය සිහිපත් කරන්නේ නම්
මෙම රූපයේ එය 720 ° ට සමාන බව පෙනේ. හොඳයි, රූපයේ සියලුම කෝණ සමාන බැවින්, ඒ සෑම එකක්ම 120 ° ට සමාන බව ගණනය කිරීම පහසුය.
ෂඩාස්රයක් ඇඳීම ඉතා සරලයි, ඔබට අවශ්ය වන්නේ මාලිමා යන්ත්රයක් සහ පාලකයෙකු පමණි.
පියවරෙන් පියවර උපදෙස් මේ ආකාරයෙන් පෙනෙනු ඇත:
අවශ්ය නම්, සමාන අරය සහිත රවුම් පහක් ඇඳීමෙන් ඔබට රේඛාවක් නොමැතිව කළ හැකිය.
මෙලෙස ලබාගත් රූපය නිත්ය ෂඩාස්රයක් වන අතර මෙය පහතින් ඔප්පු කළ හැක.
දේපල සරල හා රසවත් ය
නිත්ය ෂඩාස්රයක ගුණ තේරුම් ගැනීමට, එය ත්රිකෝණ හයකට කැඩීම අර්ථවත් කරයි:
අනාගතයේදී එහි ගුණාංග වඩාත් පැහැදිලිව පෙන්වීමට මෙය උපකාරී වනු ඇත, ඒවායින් ප්‍රධාන වන්නේ:
- වටකුරු රවුම් විෂ්කම්භය;
- ලියා ඇති කවයේ විෂ්කම්භය;
- හතරැස්;
- පරිමිතිය.
වටකුරු කවය සහ ඉදිකිරීම් හැකියාව
ෂඩාස්රයක් වටා කවයක් විස්තර කළ හැකි අතර, එපමනක් නොව, එකක් පමණි. මෙම රූපය නිවැරදි බැවින්, ඔබට එය ඉතා සරලව කළ හැකිය: ඇතුළත යාබද කෝණ දෙකකින් බයිසෙක්ටරයක් අඳින්න. ඒවා O ලක්ෂ්‍යයේදී ඡේදනය වන අතර, ඒවා අතර පැත්ත සමඟ එක්ව ත්රිකෝණයක් සාදයි.
ෂඩාස්‍රයේ පැත්ත සහ ද්විභාණ්ඩ අතර කෝණ 60° බැගින් වනු ඇත, එබැවින් අපට නියත වශයෙන්ම කිව හැක්කේ ත්රිකෝණයක්, උදාහරණයක් ලෙස, AOB, සමද්වීපක්ෂ බවයි. තුන්වන කෝණය ද 60 ° ට සමාන වන බැවින් එය ද සමපාර්ශ්වික වේ. එයින් කියවෙන්නේ OA සහ OB කොටස් සමාන වන අතර එයින් අදහස් කරන්නේ ඒවාට රවුමේ අරය ලෙස සේවය කළ හැකි බවයි.
ඊට පසු, ඔබට ඊළඟ පැත්තට යා හැකි අතර, C ලක්ෂයේ කෝණයෙන් ද්විභාණ්ඩයක් ද අඳින්න. එය තවත් සමපාර්ශ්වික ත්රිකෝණයක් බවට පත් වනු ඇති අතර, AB පැත්ත එකවර දෙකට පොදු වන අතර, OS යනු එම කවයම ගමන් කරන මීළඟ අරය වනු ඇත. සමස්තයක් වශයෙන් එවැනි ත්රිකෝණ හයක් පවතිනු ඇති අතර, O ලක්ෂ්‍යයේ ඒවාට පොදු ශීර්ෂයක් ඇත. එය රවුම විස්තර කිරීමට හැකි වනු ඇති අතර එය එකක් පමණක් වන අතර එහි අරය ෂඩාස්‍රයේ පැත්තට සමාන වේ. :
මාලිමා යන්ත්රයක් සහ පාලකයෙකු ආධාරයෙන් මෙම රූපය ගොඩනගා ගත හැක්කේ එබැවිනි.
හොඳයි, මෙම කවයේ ප්රදේශය සම්මත වනු ඇත:
ලියා ඇති කවය
වටකුරු රවුමේ කේන්ද්‍රය සෙල්ලිපියේ කේන්ද්‍රය සමඟ සමපාත වේ. මෙය සත්‍යාපනය කිරීම සඳහා, අපට O ලක්ෂ්‍යයේ සිට ෂඩාස්‍රයේ දෙපැත්තට ලම්බක අඳින්න පුළුවන්. ඒවා ෂඩාස්‍රය සෑදෙන එම ත්‍රිකෝණවල උස වනු ඇත. සමද්වීපාද ත්රිකෝණයක උස යනු එය රැඳෙන පැත්තට සාපේක්ෂව මධ්‍යයයි. මේ අනුව, මෙම උස යනු ශිලාලේඛන රවුමේ අරය වන ලම්බක ද්වි අංශය මිස අන් කිසිවක් නොවේ.
සමපාර්ශ්වික ත්රිකෝණයක උස සරලව ගණනය කරනු ලැබේ:
h²=a²-(a/2)²= a²3/4, h=a(√3)/2
R=a සහ r=h නිසා, එය හැරෙනවා
r=R(√3)/2.
මේ අනුව, සෙල්ලිපි කරන ලද කවය නිත්ය ෂඩාස්රයක පැතිවල කේන්ද්‍ර හරහා ගමන් කරයි.
එහි ප්රදේශය වනු ඇත:
S=3πa²/4,
එනම්, විස්තර කරන ලද ඉන් හතරෙන් තුනක්.
පරිමිතිය සහ ප්රදේශය
පරිමිතිය සමඟ සෑම දෙයක්ම පැහැදිලිය, මෙය පැතිවල දිග එකතුවකි:
P=6a, හෝ P=6R
නමුත් ප්රදේශය ෂඩාස්‍රය බෙදිය හැකි ත්රිකෝණ හයේම එකතුවට සමාන වේ. ත්රිකෝණයක වර්ගඵලය පාදයේ සහ උසෙහි ගුණිතයෙන් අඩක් ලෙස ගණනය කරනු ලබන බැවින්, එසේ නම්:
S \u003d 6 (a / 2) (a (√3) / 2) \u003d 6a² (√3) / 4 \u003d 3a² (√3) / 2හෝ
S=3R²(√3)/2
ලියා ඇති කවයේ අරය හරහා මෙම ප්රදේශය ගණනය කිරීමට කැමති අයට මේ ආකාරයට කළ හැකිය:
S=3(2r/√3)²(√3)/2=r²(2√3)
විනෝදාත්මක ඉදිකිරීම්
ත්රිකෝණයක් ෂඩාස්රයක සටහන් කළ හැකි අතර, එහි පැති එකකින් සිරස් සම්බන්ධ කරයි:
සමස්තයක් වශයෙන් ඔවුන්ගෙන් දෙදෙනෙකු සිටින අතර, ඔවුන් එකිනෙකා මත පැටවීම දාවිත්ගේ තාරකාව ලබා දෙනු ඇත. මෙම සෑම ත්‍රිකෝණයක්ම සමපාර්ශ්වික වේ. මෙය සත්‍යාපනය කිරීම පහසුය. ඔබ AC පැත්ත දෙස බැලුවහොත්, එය එකවර ත්රිකෝණ දෙකකට අයත් වේ - BAC සහ AEC. ඒවායින් පළමුවැන්න AB \u003d BC නම් සහ ඒවා අතර කෝණය 120 ° වේ නම්, ඉතිරි එක් එක් ඒවා 30 ° වේ. මෙයින් අපට තාර්කික නිගමන උකහා ගත හැකිය:
- sin30°=1/2 සිට ABC හි උස B ශීර්ෂයේ සිට ෂඩාස්‍රයේ අඩකට සමාන වේ. මෙය සත්‍යාපනය කිරීමට කැමති අයට පයිතගරස් ප්‍රමේයය අනුව නැවත ගණනය කිරීමට උපදෙස් දිය හැකිය, එය මෙහි හොඳින් ගැලපේ.
- AC පැත්ත නැවතත් එම ප්‍රමේයය භාවිතා කර ගණනය කරන ලද සෙල්ලිපි රවුමේ අරය දෙකකට සමාන වේ. එනම්, AC=2(a(√3)/2)=a(√3).
- ABC, CDE සහ AEF යන ත්රිකෝණ පැති දෙකකින් සමාන වන අතර ඒවා අතර කෝණය සමාන වන අතර එම නිසා AC, CE සහ EA යන පැතිවල සමානාත්මතාවය පහත දැක්වේ.
එකිනෙකා සමඟ ඡේදනය වීම, ත්රිකෝණ නව ෂඩාස්රයක් සාදන අතර, එය ද නිතිපතා වේ. ඔප්පු කිරීම පහසුය:
මේ අනුව, රූපය නිත්ය ෂඩාස්රයක සලකුණු හමු වේ - එයට සමාන පැති සහ කෝණ හයක් ඇත. සිරස්වල ඇති ත්‍රිකෝණවල සමානාත්මතාවයෙන්, නව ෂඩාස්‍රයේ පැත්තේ දිග අඩු කිරීම පහසුය:
d=а(√3)/3
එය වටා විස්තර කර ඇති රවුමේ අරය ද වනු ඇත. ABC ත්රිකෝණය සලකා බැලීමේදී ඔප්පු වූ විශාල ෂඩාස්‍රයේ පැත්තේ අඩක් සෙල්ලිපියේ අරය වනු ඇත. එහි උස හරියටම පැත්තේ අඩකි, එබැවින් දෙවන භාගය කුඩා ෂඩාස්‍රයේ කොටා ඇති රවුමේ අරය වේ:
r₂=A/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
ඩේවිඩ් තාරකාව තුළ ඇති ෂඩාස්‍රයේ ප්රදේශය තාරකාව ලියා ඇති විශාල ප්‍රමාණයට වඩා තුන් ගුණයකින් කුඩා බව පෙනේ.
න්‍යායේ සිට භාවිතය දක්වා
ෂඩාස්‍රයේ ගුණාංග ස්වභාවධර්මයේ මෙන්ම මානව ක්‍රියාකාරකම්වල විවිධ ක්ෂේත්‍රවලද ඉතා ක්‍රියාකාරීව භාවිතා වේ. පළමුවෙන්ම, මෙය බෝල්ට් සහ ඇට වර්ග සඳහා අදාළ වේ - ඔබ චැම්ෆර් සැලකිල්ලට නොගන්නේ නම්, පළමු හා දෙවන තොප්පි සාමාන්‍ය ෂඩාස්‍රයකට වඩා වැඩි දෙයක් නොවේ. ප්රමාණය යතුරලියා ඇති කවයේ විෂ්කම්භයට අනුරූප වේ - එනම් ප්‍රතිවිරුද්ධ මුහුණු අතර දුර.
එහි යෙදුම සහ ෂඩාස්රාකාර ටයිල් සොයාගෙන ඇත. එය හතරැස් එකකට වඩා බෙහෙවින් අඩු ය, නමුත් එය තැබීම වඩාත් පහසු වේ: උළු තුනක් එක් ස්ථානයක හමු වේ, හතරක් නොවේ. සංයුතිය ඉතා රසවත් විය හැකිය:
කොන්ක්රීට් අතුරන ස්ලැබ් ද නිෂ්පාදනය කෙරේ.
ස්වභාවධර්මයේ ෂඩාස්‍රයේ පැතිරීම සරලව පැහැදිලි කර ඇත. මේ අනුව, රවුම් සහ බෝල එකම විෂ්කම්භයක් තිබේ නම් ගුවන් යානයක තදින් සවි කිරීම පහසුය. මේ නිසා පැණි වදවලට එවැනි හැඩයක් තිබේ.
