เวกเตอร์: คำจำกัดความและแนวคิดพื้นฐาน การใช้เวกเตอร์ในชีวิตประจำวัน กฎสำหรับการทำงานกับเวกเตอร์

เวกเตอร์. การดำเนินการข้างบนเวกเตอร์ สเกลาร์

เวกเตอร์ ผลิตภัณฑ์ผสมของเวกเตอร์

1. เวกเตอร์ การดำเนินการกับเวกเตอร์

คำจำกัดความพื้นฐาน

คำจำกัดความ 1.ปริมาณที่มีลักษณะครบถ้วนด้วยค่าตัวเลขในระบบหน่วยที่เลือกเรียกว่า สเกลาร์หรือ สเกลาร์ .

(น้ำหนักตัว ปริมาตร เวลา ฯลฯ)

คำจำกัดความ 2ปริมาณที่แสดงด้วยค่าตัวเลขและทิศทางเรียกว่า เวกเตอร์ หรือ เวกเตอร์ .

(การกระจัด แรง ความเร็ว ฯลฯ)

ชื่อ: , หรือ , .

เวกเตอร์เรขาคณิตเป็นส่วนที่กำกับ

สำหรับเวกเตอร์ - จุด ก- จุดเริ่มต้น ในเป็นจุดสิ้นสุดของเวกเตอร์

นิยาม 3.โมดูล เวกเตอร์คือความยาวของส่วน AB

ความหมาย 4.เรียกว่าเวกเตอร์ที่มีโมดูลัสเป็นศูนย์ ศูนย์ , ระบุไว้

คำจำกัดความ 5.เวกเตอร์ที่อยู่บนเส้นขนานหรือบนเส้นเดียวกัน เรียกว่า เวกเตอร์ คอลิเนียร์ . ถ้าเวกเตอร์คอลลิเนียร์สองตัวมีทิศทางเดียวกัน ก็จะเรียกว่า ร่วมทิศทาง .

คำจำกัดความ 6.พิจารณาเวกเตอร์สองตัว เท่ากัน , ถ้าพวกเขา ร่วมกำกับ และมีค่าโมดูลัสเท่ากัน

การดำเนินการกับเวกเตอร์

1) การบวกเวกเตอร์

เดฟ 6.ผลรวม เวกเตอร์สองตัวและเป็นเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่สร้างจากเวกเตอร์เหล่านี้ ซึ่งมาจากจุดร่วมของการประยุกต์ (กฎสี่เหลี่ยมด้านขนาน).

รูปที่ 1

เดฟ 7.ผลรวมของเวกเตอร์สามตัว , , คือเส้นทแยงมุมของเส้นขนานที่สร้างขึ้นบนเวกเตอร์เหล่านี้ (กฎคู่ขนาน).

เดฟ 8.ถ้า ก, ใน, กับ เป็นจุดโดยพลการ แล้ว + = (กฎสามเหลี่ยม).

รูปที่ 2

คุณสมบัติเพิ่มเติม

1 อ . + = + (กฎหมายการกระจัด).

2 อ . + ( + ) = ( + ) + = ( + ) + (กฎหมายที่เกี่ยวข้อง).

3 อ . + (– ) + .

2) การลบเวกเตอร์

เดฟ 9.ภายใต้ ความแตกต่าง เวกเตอร์และเข้าใจเวกเตอร์ = - อย่างนั้น + = .

ในสี่เหลี่ยมด้านขนาน นี่คืออีกอันหนึ่ง เส้นทแยงมุม SD (ดูรูปที่ 1)

3) การคูณเวกเตอร์ด้วยจำนวน

เดฟ 10. งาน เวกเตอร์เป็นสเกลาร์ เค เรียกว่าเวกเตอร์

= เค = เค ,

ยาว คะ , และทิศทางซึ่ง:

1. ตรงกับทิศทางของเวกเตอร์ถ้า เค > 0;

2. ตรงข้ามกับทิศทางของเวกเตอร์ if เค < 0;

3. โดยพลการถ้า เค = 0.

คุณสมบัติของการคูณเวกเตอร์ด้วยจำนวน

1 อ . (เค + ล ) = เค + ล .

เค ( + ) = เค + เค .

2 โอ . เค (ล ) = (KL ) .

3 โอ . 1  = , (–1)  = – , 0  = .

คุณสมบัติของเวกเตอร์

เดฟ สิบเอ็ดเวกเตอร์สองตัวและถูกเรียก คอลิเนียร์ หากตั้งอยู่บน เส้นขนานหรือที่ เส้นตรงหนึ่งเส้น

เวกเตอร์ศูนย์นั้นใกล้เคียงกับเวกเตอร์ใดๆ

ทฤษฎีบท 1.เวกเตอร์สองตัวที่ไม่ใช่ศูนย์ และ คอลิเนียร์,  เมื่อพวกมันเป็นสัดส่วนเช่น

= เค , เค - สเกลาร์

เดฟ 12.เวกเตอร์สามตัว , , เรียกว่า ระนาบเดียวกัน ถ้าพวกมันขนานกับระนาบหรืออยู่ในระนาบนั้น

ทฤษฎีบท 2สามเวกเตอร์ที่ไม่ใช่ศูนย์ , , ระนาบ,  เมื่อหนึ่งในนั้นเป็นผลรวมเชิงเส้นของอีกสองตัว นั่นคือ

= เค + ล , เค , ล - สเกลาร์

การฉายเวกเตอร์บนแกน

ทฤษฎีบท 3การฉายเวกเตอร์บนแกน (เส้นตรง) ลเท่ากับผลคูณของความยาวของเวกเตอร์และโคไซน์ของมุมระหว่างทิศทางของเวกเตอร์และทิศทางของแกน เช่น = ก  คระบบปฏิบัติการ  ,  = ( , ล).

2. พิกัดเวกเตอร์

เดฟ 13.การฉายภาพเวกเตอร์บนแกนพิกัด โอ้, อู๋, ออนซ์เรียกว่า พิกัดเวกเตอร์ ชื่อ:  ก x , ก ย , ก ซี .

ความยาวเวกเตอร์:

ตัวอย่าง:คำนวณความยาวของเวกเตอร์

สารละลาย:

ระยะห่างระหว่างจุด และ คำนวณโดยสูตร: .

ตัวอย่าง:ค้นหาระยะห่างระหว่างจุด M (2,3,-1) และ K (4,5,2)

การดำเนินการกับเวกเตอร์ในรูปแบบพิกัด

ให้เวกเตอร์ = ก x , ก ย , ก ซี และ = ข x , ข ย , ข ซี .

1. (  )= ก x  ข x , ก ย  ข ย , ก ซี  ข ซี .

2.  =   ก x ,  ก ย ,  ก ซี ที่ไหน  - สเกลาร์

ผลคูณสเกลาร์ของเวกเตอร์

คำนิยาม:ภายใต้ผลคูณสเกลาร์ของสองเวกเตอร์และ

เป็นที่เข้าใจกันว่าเป็นตัวเลขที่เท่ากับผลคูณของความยาวของเวกเตอร์เหล่านี้และโคไซน์ของมุมระหว่างพวกมัน เช่น = , - มุมระหว่างเวกเตอร์และ .

คุณสมบัติของดอทโปรดักส์:

1.  =

2. ( + ) =

5. สเกลาร์อยู่ที่ไหน

6. เวกเตอร์สองตัวตั้งฉากกัน (ตั้งฉาก) ถ้า .

7. ถ้าและถ้าเท่านั้น .

ผลคูณสเกลาร์ในรูปแบบพิกัดมีรูปแบบ: , ที่ไหนและ .

ตัวอย่าง:ค้นหาผลคูณสเกลาร์ของเวกเตอร์และ

สารละลาย:

เวกเตอร์ถือเวกเตอร์

คำนิยาม: ผลคูณเวกเตอร์ของสองเวกเตอร์และเข้าใจว่าเป็นเวกเตอร์ที่:

โมดูลนี้เท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์เหล่านี้ เช่น , มุมระหว่างเวกเตอร์และ

เวกเตอร์นี้ตั้งฉากกับเวกเตอร์ที่คูณ นั่นคือ

ถ้าเวกเตอร์ไม่เป็นเส้นตรง มันจะสร้างเวกเตอร์สามตัวที่ถูกต้อง

ข้ามคุณสมบัติของผลิตภัณฑ์:

1. เมื่อลำดับของปัจจัยเปลี่ยนไป ผลคูณเวกเตอร์จะเปลี่ยนเครื่องหมายเป็นตรงกันข้าม โดยคงโมดูลไว้ เช่น

2 .Vector square เท่ากับ zero-vector เช่น

3 . สามารถนำปัจจัยสเกลาร์ออกจากเครื่องหมายของผลิตภัณฑ์เวกเตอร์ได้ เช่น

4 .สำหรับเวกเตอร์สามตัวใด ๆ ความเท่าเทียมกัน

5 เงื่อนไขที่จำเป็นและเพียงพอสำหรับความสัมพันธ์เชิงเส้นของสองเวกเตอร์และ :

ผลิตภัณฑ์เวกเตอร์ในรูปแบบพิกัด

ถ้าพิกัดของเวกเตอร์และ , จากนั้นจะพบผลิตภัณฑ์เวกเตอร์ของพวกเขาโดยสูตร:

จากนั้นจากคำจำกัดความของผลิตภัณฑ์ข้ามเป็นไปตามพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างขึ้นจากเวกเตอร์และคำนวณโดยสูตร:

ตัวอย่าง:คำนวณพื้นที่ของสามเหลี่ยมที่มีจุดยอด (1;-1;2), (5;-6;2), (1;3;-1)

สารละลาย: .

จากนั้นพื้นที่ของสามเหลี่ยม ABC จะถูกคำนวณดังนี้:

ผลคูณของเวกเตอร์

คำนิยาม:ผลคูณของเวกเตอร์ (เวกเตอร์สเกลาร์) แบบผสมคือตัวเลขที่กำหนดโดยสูตร: .

คุณสมบัติของผลิตภัณฑ์ผสม:

1. ผลิตภัณฑ์แบบผสมจะไม่เปลี่ยนแปลงตามการเปลี่ยนแปลงของปัจจัยต่างๆ เช่น .

2. เมื่อสองปัจจัยที่อยู่ใกล้เคียงแลกเปลี่ยนกัน ผลิตภัณฑ์ผสมจะเปลี่ยนสัญลักษณ์เป็นตรงกันข้าม เช่น .

3 เงื่อนไขที่จำเป็นและเพียงพอสำหรับเวกเตอร์สามตัวที่จะเป็นระนาบร่วม : =0.

4 . ผลคูณของเวกเตอร์สามตัวจะเท่ากับปริมาตรของเวกเตอร์ขนานที่สร้างขึ้นบนเวกเตอร์เหล่านี้ ใช้เครื่องหมายบวกหากเวกเตอร์เหล่านี้ประกอบกันเป็นสามเท่าทางขวา และด้วยเครื่องหมายลบหากพวกมันก่อตัวเป็นสามทางซ้าย เช่น .

ถ้ารู้จัก พิกัดเวกเตอร์ , จากนั้นจะพบผลิตภัณฑ์ผสมตามสูตร:

ตัวอย่าง:คำนวณผลคูณของเวกเตอร์

สารละลาย:

3. พื้นฐานของระบบเวกเตอร์

คำนิยาม.ระบบของเวกเตอร์เป็นที่เข้าใจกันว่าเป็นเวกเตอร์หลายตัวที่อยู่ในปริภูมิเดียวกัน ร.

ความคิดเห็นหากระบบประกอบด้วยเวกเตอร์จำนวนจำกัด พวกมันจะแสดงด้วยตัวอักษรเดียวกันโดยมีดัชนีต่างกัน

ตัวอย่าง.

คำนิยาม. เวกเตอร์ใดๆ ในรูปแบบ = เรียกว่าผลรวมเชิงเส้นของเวกเตอร์ ตัวเลขคือค่าสัมประสิทธิ์ของการรวมกันเชิงเส้น

ตัวอย่าง. .

คำนิยาม. ถ้าเวกเตอร์เป็นผลรวมเชิงเส้นของเวกเตอร์ , แล้วเราบอกว่าเวกเตอร์แสดงเป็นเส้นตรงในรูปของเวกเตอร์ .

คำนิยาม.ระบบเวกเตอร์เรียกว่า อิสระเชิงเส้นหากไม่มีเวกเตอร์ใดในระบบที่สามารถรวมกันเป็นเชิงเส้นของเวกเตอร์ที่เหลือได้ มิฉะนั้น ระบบจะเรียกว่าขึ้นอยู่กับเชิงเส้น

ตัวอย่าง. ระบบเวกเตอร์ ขึ้นอยู่กับเชิงเส้นตั้งแต่เวกเตอร์ .

คำจำกัดความพื้นฐานระบบเวกเตอร์เป็นพื้นฐานหาก:

1) มันเป็นอิสระเชิงเส้น

2) เวกเตอร์ของพื้นที่ผ่านจะแสดงเป็นเส้นตรง

ตัวอย่างที่ 1พื้นฐานพื้นที่: .

2. ในระบบเวกเตอร์ เวกเตอร์เป็นพื้นฐาน: , เพราะ แสดงเชิงเส้นในรูปของเวกเตอร์

ความคิดเห็นในการค้นหาพื้นฐานของระบบเวกเตอร์ที่กำหนด คุณต้อง:

1) เขียนพิกัดของเวกเตอร์ในเมทริกซ์

2) ใช้การแปลงเบื้องต้น นำเมทริกซ์มาอยู่ในรูปสามเหลี่ยม

3) แถวที่ไม่ใช่ศูนย์ของเมทริกซ์จะเป็นพื้นฐานของระบบ

4) จำนวนเวกเตอร์ในฐานเท่ากับอันดับของเมทริกซ์

1. นอกจากนี้ ให้ a และ b เป็นเวกเตอร์สองตัว จากจุด O โดยพลการ เราแยกเวกเตอร์ OA = a และจากจุดผลลัพธ์ A - เวกเตอร์ AB = b เวกเตอร์ OB เรียกว่าผลรวมก+ ขเวกเตอร์ a และ b (รูปที่ 6) และการดำเนินการหาผลรวมของเวกเตอร์คือการบวก

ให้เราตรวจสอบว่าการบวกเวกเตอร์ถูกกำหนดอย่างถูกต้อง เช่น ผลรวมของเวกเตอร์ไม่ได้ขึ้นอยู่กับตัวเลือกของจุด O ในการทำเช่นนี้ ให้นำจุด Q อื่น ๆ มาวางไว้และแยกเวกเตอร์ QC = a และ CD = b เนื่องจาก QC = OA = a โดยเกณฑ์ความเท่าเทียมกันของเวกเตอร์สองตัว (1.8) เราได้ OQ = AC นั้น ในทำนองเดียวกันจากความเท่าเทียมกัน AB = CD = b จะได้ว่า AC = BD ดังนั้น OQ = BD และใช้เกณฑ์อีกครั้ง (1.8) เราได้รับ OB = QD ซึ่งจะต้องได้รับการพิสูจน์ (รูปที่ 7)

กฎสามเหลี่ยมต่อท้ายโดยตรงจากนิยามของผลรวมของเวกเตอร์สองตัว:

(2.1) สำหรับสามจุด O, A และ B OA + AB = OB

นอกจากนี้ ตามที่ทราบจากหลักสูตรเรขาคณิตของโรงเรียน สำหรับสามจุด O, A และ B ความยาวของส่วน OB ไม่เกินผลรวมของความยาวของส่วน OA และ AB และความเท่ากัน |OB| = |OA| + |AB| จะไปถึงก็ต่อเมื่อจุด A อยู่บนส่วน [OB] ความไม่เท่าเทียมกันนี้มักเรียกว่าอสมการรูปสามเหลี่ยม คำจำกัดความของผลรวมของเวกเตอร์ทำให้คุณสามารถเขียนในรูปแบบเวกเตอร์ได้:

(2.2) |а + ข| |ก| + |ข| .

ความเท่าเทียมกันใน (2.2) จะเกิดขึ้นก็ต่อเมื่อเวกเตอร์ a และ b อยู่ในทิศทางเดียวกัน และในกรณีอื่น ๆ อสมการจะเคร่งครัด เขียนความเท่าเทียมกัน |a+b| = |ก|+|ข| สำหรับเวกเตอร์โดยพลการ - ข้อผิดพลาดขั้นต้น

2. คุณสมบัติพื้นฐานของการบวกเวกเตอร์ เหล่านี้รวมถึง:

(C1) สำหรับเวกเตอร์สามตัวใดๆ a, b และ c (a+b)+c = a+(b+c) (การเชื่อมโยง)

(С2) สำหรับเวกเตอร์สองตัวใดๆ a และ b a+b = b+a (การสลับที่)

(С3) สำหรับเวกเตอร์ใดๆ a+0 = a

(C4) สำหรับสองจุด A และ B AB + BA = 0

ใน

ในมุมมองของคุณสมบัติหลัง เวกเตอร์ BA และ AB เรียกว่าตรงกันข้าม เวกเตอร์ตรงข้ามกับเวกเตอร์ a เขียนแทนด้วย "-a"



คุณสมบัติ (C3) และ (C4) ติดตามโดยตรงจากกฎสามเหลี่ยม (ตรวจสอบ!) เพื่อพิสูจน์ (C2) จากจุด O โดยพลการ เราแยกเวกเตอร์ OA = a และ OS = b และจากจุด A - เวกเตอร์ AB = b (รูปที่ 8) เนื่องจาก OS \u003d AB โดยเครื่องหมายของความเท่าเทียมกันของสองส่วนที่กำกับ เราจึงได้ OA \u003d CB นั้น แต่ OA \u003d a ดังนั้นจึงเป็น CB ด้วย = ก. โปรดทราบว่าตามกฎสามเหลี่ยม เวกเตอร์ OB สามารถแสดงได้ทั้งเป็น OA + OB = a + b และ OC + CB = b + a ปรากฎว่า a + b = b + a = OS ซึ่งจำเป็นต้องได้รับการพิสูจน์

ให้เราพิสูจน์ทรัพย์สิน (С1) ในการทำเช่นนี้ เราเลื่อนเวกเตอร์ OA = a, AB = b และ BC = c ตามลำดับ ตามนิยามของการบวกเวกเตอร์ (a + b) + c = OB + BC และ a + (b + c) = OA + AC แต่ OB + BC \u003d OA + AC \u003d OS (รูปที่ 9)

โปรดทราบว่าในรูปที่ 8อค = เอบี. ดังนั้นจึงยุติธรรม

(2.3) กฎสี่เหลี่ยมด้านขนาน: ผลรวมของเวกเตอร์ที่ไม่ใช่เส้นตรง a และ b เท่ากับ OB ในแนวทแยงของ OABS สี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์ 2 OA = a และ OS = b

นอกจากนี้ เราได้รับจากหลักฐานการเชื่อมโยงข้างต้น

(2.4) กฎรูปหลายเหลี่ยม ในการเพิ่มเวกเตอร์หลายตัวตามลำดับที่แน่นอน เราต้องวางพวกมันไว้ข้างๆ กันเพื่อให้จุดสิ้นสุดของเวกเตอร์แต่ละตัวทำหน้าที่เป็นจุดเริ่มต้นของเวกเตอร์ถัดไป จากนั้นจึงเชื่อมจุดเริ่มต้นของเวกเตอร์แรกเข้ากับจุดสิ้นสุดของเวกเตอร์สุดท้าย

เราได้พิสูจน์กฎนี้เฉพาะในกรณีของเวกเตอร์สามตัวเท่านั้น แต่เหตุผลข้างต้นสามารถขยายไปถึงเงื่อนไขจำนวนเท่าใดก็ได้

พี

เนื่องจากจุดเริ่มต้นของส่วนที่กำกับด้วยศูนย์ตรงกับจุดสิ้นสุด ผลลัพธ์ที่เป็นประโยชน์จึงตามมาจากกฎรูปหลายเหลี่ยม

(2.5) กฎลูกโซ่แบบปิด ผลรวมของเวกเตอร์หลายตัวจะเท่ากับศูนย์ก็ต่อเมื่อ เมื่อพวกเขาถูกเลื่อนออกไปตามลำดับ พวกมันก่อตัวเป็นห่วงโซ่ปิด นั่นคือ จุดจบของสิ่งหลังเกิดขึ้นพร้อมกับการเริ่มต้นของสิ่งแรก

(2.6) การออกกำลังกาย พิสูจน์กฎของเส้นขนาน: ในการเพิ่มเวกเตอร์สามตัวที่ไม่ขนานกับระนาบเดียวกัน คุณต้องแยกพวกมันออกจากจุด O จุดหนึ่ง ทำส่วนที่เป็นผลลัพธ์สามส่วนให้เป็นเส้นขนาน และวาดเส้นทแยงมุมของเส้นขนานนี้จากจุด O ซึ่งจะเป็นผลรวมที่ต้องการ (รูปที่ 10)

การเชื่อมโยงของการบวกเวกเตอร์แสดงให้เห็นว่าผลรวมของเวกเตอร์สามตัวที่เรียงลำดับกัน ไม่ได้ขึ้นอยู่กับว่าเราเพิ่มเวกเตอร์สองตัวแรกก่อน แล้วจึงบวกเวกเตอร์ที่สามเข้าไป หรือหาผลรวมของเวกเตอร์ที่สองและสามก่อน เวกเตอร์ แล้วบวกเข้าไปที่ตัวแรก ซึ่งหมายความว่าเราสามารถเขียนผลรวมของเวกเตอร์สามตัวเป็น a + b + c ได้โดยไม่ต้องคิดว่าจะใส่วงเล็บลงไปอย่างไร ในวิชาพีชคณิต จะเห็นว่าหากคุณสมบัตินี้มีสามพจน์ มันก็จะคงอยู่สำหรับจำนวนเท่าใดก็ได้ นั่นคือ เราสามารถเขียนผลบวกเวกเตอร์ใดๆ a + b + c + ... + ได้โดยไม่ต้องกังวล เกี่ยวกับวิธีการวางวงเล็บ ง. และคุณสมบัติการสลับสับเปลี่ยน (C2) แสดงให้เห็นว่าเราสามารถจัดเรียงเงื่อนไขใหม่โดยพลการได้โดยไม่ต้องเปลี่ยนผลรวมนี้ นี่คือความหมายของการเชื่อมโยงและการแลกเปลี่ยน

. การลบเวกเตอร์ ผลต่าง a–b ของเวกเตอร์ a และ b คือเวกเตอร์ x โดยที่ x+b = a การดำเนินการค้นหาความแตกต่างของเวกเตอร์เรียกว่าการลบ

ให้เราแยกเวกเตอร์ OA=a และ OB=b ออกจากจุด O ตามอำเภอใจ เห็นได้ชัดว่าเวกเตอร์เดียวที่ให้ OA ร่วมกับ OB คือเวกเตอร์ BA ดังนั้น,

(2.7) เวกเตอร์สองตัวใด ๆ มีความแตกต่างและมีเพียงหนึ่งเดียว ในการสร้างคุณต้องเลื่อนเวกเตอร์ออกจากจุดหนึ่งและเชื่อมต่อจุดสิ้นสุดของจุดที่สองกับจุดสิ้นสุดของจุดแรก (รูปที่ 11)

ว

เรายังทราบด้วยว่าในรูป 11 VA = บีโอ + โอเอ มันหมายความว่า

ก–ข = ก+(–ข).

กล่าวอีกนัยหนึ่ง การลบเวกเตอร์หนึ่งออกจากอีกเวกเตอร์หนึ่งก็เหมือนกับการบวกเวกเตอร์แรกเข้ากับเวกเตอร์ตรงข้ามของเวกเตอร์ที่สอง

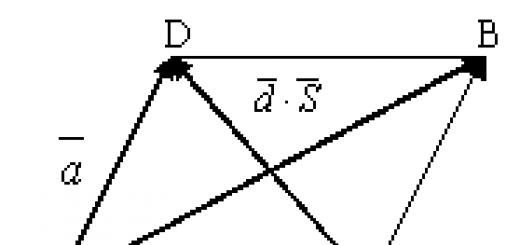
ให้เวกเตอร์ a และ b ไม่เป็นเส้นตรง จากนั้นจุด O, A และ B จะสร้างรูปสามเหลี่ยม หากเราทำให้เป็นสี่เหลี่ยมด้านขนาน OASV เส้นทแยงมุมก็จะอยู่ในนั้น
จะเป็นตัวแทนของผลรวม a + b และเส้นทแยงมุม
- ความแตกต่าง a-b (รูปที่ 12) นี่เป็นส่วนเพิ่มเติมที่มีประโยชน์สำหรับกฎสี่เหลี่ยมด้านขนาน

ความเท่าเทียมกัน (2.8) สามารถพิสูจน์ได้ด้วยพีชคณิตล้วน แน่นอน ถ้า x = a+(–b) แล้ว x+b = a+(–b)+b = a+0 = ก. นอกจากนี้ยังสามารถแสดงได้ในเชิงพีชคณิตว่าผลต่าง a–b ไม่มีค่าอื่น: x+b = ก (x+b)+(–b) = ก+(–ข) x+(b+(–b)) = a+(–b) x+0=ก+(–ข) x = a+(–b). เราจงใจเขียนการเปลี่ยนแปลงเหล่านี้ทั้งหมดโดยละเอียดเพื่อแสดงว่าการเปลี่ยนแปลงเหล่านี้อาศัยคุณสมบัติพื้นฐานของการบวก (C1)-(C4) เท่านั้น (ตรวจสอบ!) ในทฤษฎีทั่วไปของปริภูมิเวกเตอร์ ซึ่งคุณจะได้เรียนรู้ในหลักสูตรพีชคณิต คุณสมบัติเหล่านี้ถือเป็นสัจพจน์ของการบวกเวกเตอร์ และคุณสมบัติอื่นๆ ทั้งหมดของการบวกได้มาจากคุณสมบัติเหล่านี้

4. การคูณเวกเตอร์ด้วยจำนวน การคูณเวกเตอร์ด้วยตัวเลขคือการดำเนินการหาผลคูณของเวกเตอร์ด้วยตัวเลข ผลคูณของเวกเตอร์ที่ไม่ใช่ศูนย์ a และจำนวน x คือเวกเตอร์แทน "xa" และตรงตามเงื่อนไขสองข้อต่อไปนี้:

(P1) | ฮา | = |x||ก| ; (P2) ฮ่า และถ้า x 0 และ ฮ่า และถ้า x<0.

ผลคูณของเวกเตอร์ศูนย์ด้วยจำนวนใดๆ ตามนิยาม เท่ากับ 0

เงื่อนไข (A1) ยังคงใช้ได้สำหรับx= 0 แต่เงื่อนไข (A2) ในกรณีนี้ถูกละเมิดที่ x<0 (из-за чего случай нулевого вектора и приходится рассматривать отдельно). Однако, при любых а и х векторы а и ха коллинеарны (почему?).

โปรดทราบว่า xa = 0 |ฮา| = 0  |x||ก| = 0  |x| = 0 หรือ |ก| = 0  เอ็กซ์ = 0 หรือ ก = 0. ดังนั้น

(2.9) ผลคูณของเวกเตอร์และจำนวนมีค่าเท่ากับศูนย์ก็ต่อเมื่อจำนวนหรือเวกเตอร์มีค่าเท่ากับศูนย์

ให้จำนวนที่ไม่ใช่ศูนย์ x และเวกเตอร์ a ได้รับ จากจุด O โดยพลการ เราแยกเวกเตอร์ OA = a และพยายามสร้างเวกเตอร์วัว= ฮา เนื่องจากเวกเตอร์ a และ xa ต้องเป็นเส้นตรง ส่วน
ต้องอยู่บนเส้นตรง (OA) และความยาวตามเงื่อนไข (A1) ต้องเท่ากับ |x||a| มีสองส่วนดังกล่าวและหนึ่งในนั้น (ขอเรียกมันว่า
) กำกับร่วมกับ
และอื่น ๆ (ขอเรียกว่า
) กำกับตรงกันข้าม
(รูปที่ 13) กลับสู่สภาพ (P2) เราจะเห็นว่า
=
สำหรับ x > 0 และ
=
ที่ x< 0.

ต

ดังนั้น เวกเตอร์ใดๆ สามารถคูณด้วยจำนวนใดๆ ก็ได้ และผลลัพธ์จะถูกกำหนดโดยไม่ซ้ำกัน

คุณสมบัติหลักของการคูณเวกเตอร์ด้วยตัวเลขมีดังต่อไปนี้:

(Y1) สำหรับเวกเตอร์ใดๆ a 1a=a (เช่น การคูณด้วย 1 จะไม่เปลี่ยนเวกเตอร์)

(Y2) สำหรับจำนวนใดๆ x, y และเวกเตอร์ a x(ya) = (xy)a (การเชื่อมโยง)

(Y3) สำหรับจำนวนใดๆ x, y และเวกเตอร์ a (x + y) a = xa + ya (การกระจายของการคูณตามการบวกของจำนวน)

(Y4) สำหรับจำนวนใดๆ x และเวกเตอร์ a และ b x(a + b) = xa + xb (การกระจายของการคูณเทียบกับการบวกของเวกเตอร์)

คุณสมบัติแรกต่อไปนี้โดยตรงจากคำจำกัดความ (ตรวจสอบ!) หลักฐานส่วนที่เหลือสามารถพบได้ในหน้า 14-16 ของ L.S. Atanasyan และ V.T. Bazylev "เรขาคณิต" (ตอนที่ 1)

เรายังสังเกตคุณสมบัติต่อไปนี้ของการคูณเวกเตอร์ด้วยตัวเลข:

(2.10) ถ้าเวกเตอร์ a ไม่ใช่ศูนย์ ดังนั้น a/|a| คือเวกเตอร์หนึ่งหน่วยที่มีทิศทางร่วมกับเวกเตอร์ a 3

 อันที่จริง เวกเตอร์ a และ a/|a| เป็นทิศทางร่วม (เพราะ 1/|a| > 0) และ |a/|a|| = |ก|/|ก| = 1.

(2.11) (–1)a = –а

 ตามนิยามของการคูณเวกเตอร์ด้วยจำนวน เวกเตอร์ (–1)a และ a จะอยู่ตรงข้ามกัน และมีความยาวเท่ากัน

5. สัญญาณของความสอดคล้องกัน

(2.12) เกณฑ์สำหรับเวกเตอร์ที่จะสอดคล้องกับเวกเตอร์ที่ไม่ใช่ศูนย์ เวกเตอร์ b มีลักษณะใกล้เคียงกับเวกเตอร์ที่ไม่ใช่ศูนย์ a ถ้าและก็ต่อเมื่อมีจำนวนนั้นอยู่ทีที่ b =ทีก. นอกจากนี้ ถ้าเวกเตอร์ a และ b เป็นทิศทางร่วม ดังนั้น t = |b| / |a| และถ้าพวกมันกำกับตรงกันข้าม t = – |ข| / |ก|.

 เราได้สังเกตแล้วว่าเวกเตอร์ a และ ta นั้นเป็นเส้นตรงเสมอ ในทางกลับกัน หาเวกเตอร์ที่ไม่ใช่ศูนย์ a และเวกเตอร์คอลลิเนียร์ b หากเป็นทิศทางร่วม เราจะใส่ t = |b|/|a| แล้ว |ตะ| = |t||а| = (|b|/|ก|)|ก| = |b| และเวกเตอร์ ta ถูกกำหนดทิศทางด้วย a และ ดังนั้น ด้วย b ดังนั้นทา = ข ตามคุณสมบัติ 1.7 ถ้า ก b เรากำหนดให้ t = –|b|/|a| และอีกครั้ง |ตะ| = |t||а| = (|b|/|ก|)|ก| = |b| ในขณะที่เวกเตอร์ ta และ b ซึ่งกำกับตรงข้ามกับเวกเตอร์ a มีทิศทางร่วมตาม (Н5) ดังนั้น ในกรณีนี้ ทะ = ข.

คำเตือนว่าเวกเตอร์ a ไม่เป็นศูนย์บางครั้งก็ไม่สะดวก จากนั้นคุณสามารถใช้สิ่งนี้

(2.13) เครื่องหมายของความสอดคล้องกันของเวกเตอร์สองตัว เวกเตอร์สองตัวจะเรียงกันเป็นเส้นตรงก็ต่อเมื่อหนึ่งในนั้นสามารถแสดงในรูปของเวกเตอร์อีกตัวหนึ่งได้โดยการคูณด้วยตัวเลข

 สำหรับกรณีที่เวกเตอร์ที่กำหนดอย่างน้อยหนึ่งในสองตัวไม่เท่ากับศูนย์ สิ่งนี้ได้รับการพิสูจน์แล้วข้างต้น หากเวกเตอร์ทั้งสองมีค่าเป็นศูนย์ ประการแรก พวกมันจะเป็นเชิงเส้นตรง และประการที่สอง พวกมันสามารถหาได้จากเวกเตอร์อื่นโดยการคูณด้วยจำนวนใด ๆ ดังนั้นในกรณีนี้ทุกอย่างเป็นไปตามลำดับ

6. การรักษาความขนานในการทำงานกับเวกเตอร์

(2.14) บทแทรกเรื่องความเท่าเทียม ถ้าเวกเตอร์สองตัวขนานกับเส้นตรง (ระนาบ) เส้นเดียวกัน (ระนาบ) จะขนานกับผลบวก ถ้าเวกเตอร์ขนานกับเส้น (ระนาบ) เส้นเดียวกัน (ระนาบ) จะขนานกับผลคูณด้วยจำนวนเท่าใดก็ได้

 ให้เวกเตอร์ a และ b ขนานกับเส้นตรงที่กำหนด (ระนาบ) ให้เราแยกออกจากจุดโดยพลการ O เวกเตอร์ OA = a และ AB = b จากนั้นจุด A และ B จะอยู่บนเส้นนี้ด้วย (ระนาบ) ซึ่งหมายความว่าส่วน OB จะอยู่ที่นั่นด้วย ซึ่งเป็นตัวแทนของผลรวม a + b ซึ่งหมายความว่าขนานกับเส้นตรง (ระนาบ)

ตอนนี้ให้เราหาจำนวน x ใดๆ และแยกเวกเตอร์ OS = xa จากจุด O เดิม ถ้า a \u003d 0 แล้ว xa \u003d 0 และเวกเตอร์ศูนย์ขนานกับเส้นและระนาบใดๆ ถ้าไม่เช่นนั้น Segment OS ซึ่งเป็นตัวแทนของเวกเตอร์ xa จะอยู่บนเส้นตรง OA ทั้งหมด ดังนั้น บนเส้นตรงที่กำหนด (ระนาบ) ดังนั้น เวกเตอร์ xa จะขนานกับเส้นนี้ (ระนาบ)

เวกเตอร์ การดำเนินการกับเวกเตอร์ ในบทความนี้ เราจะพูดถึงว่าเวกเตอร์คืออะไร วิธีหาความยาว และวิธีคูณเวกเตอร์ด้วยตัวเลข ตลอดจนวิธีหาผลรวม ผลต่าง และผลคูณดอทของเวกเตอร์สองตัว

ตามปกติแล้ว ทฤษฎีบางอย่างที่จำเป็นที่สุด

เวกเตอร์คือส่วนที่กำกับ นั่นคือ ส่วนที่มีจุดเริ่มต้นและจุดสิ้นสุด:

จุด A คือจุดเริ่มต้นของเวกเตอร์ และจุด B คือจุดสิ้นสุด

เวกเตอร์มีสองพารามิเตอร์: ความยาวและทิศทาง

ความยาวของเวกเตอร์คือความยาวของส่วนที่เชื่อมต่อจุดเริ่มต้นและจุดสิ้นสุดของเวกเตอร์ ความยาวของเวกเตอร์จะแสดง

เวกเตอร์สองตัวบอกว่าเท่ากันหากมีความยาวเท่ากันและอยู่ในแนวเดียวกัน

เวกเตอร์ทั้งสองเรียกว่า ร่วมทิศทาง, ถ้าพวกมันอยู่บนเส้นขนานและกำกับไปในทิศทางเดียวกัน: เวกเตอร์ และ กำกับร่วมกัน:

เวกเตอร์สองตัวถูกเรียกว่ากำกับตรงกันข้ามหากพวกมันอยู่บนเส้นขนานและกำกับในทิศทางตรงกันข้าม: เวกเตอร์ และ และ และ กำกับในทิศทางตรงกันข้าม:

เวกเตอร์ที่วางอยู่บนเส้นขนานเรียกว่า collinear: vectors และอยู่ใน collinear

สินค้าเวกเตอร์จำนวนนี้เรียกว่าเวกเตอร์ที่กำกับร่วมกับเวกเตอร์ ถ้า title="k>0">, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :!}

ถึง เพิ่มเวกเตอร์สองตัวและ คุณต้องเชื่อมต่อจุดเริ่มต้นของเวกเตอร์กับจุดสิ้นสุดของเวกเตอร์ ผลรวมเวกเตอร์เชื่อมต่อจุดเริ่มต้นของเวกเตอร์กับจุดสิ้นสุดของเวกเตอร์:

กฎการบวกเวกเตอร์นี้เรียกว่า กฎสามเหลี่ยม.

เพื่อเพิ่มเวกเตอร์สองตัว กฎสี่เหลี่ยมด้านขนานคุณต้องเลื่อนเวกเตอร์ออกจากจุดหนึ่งและทำให้เป็นรูปสี่เหลี่ยมด้านขนาน เวกเตอร์ผลรวมเชื่อมต่อจุดกำเนิดของเวกเตอร์กับมุมตรงข้ามของสี่เหลี่ยมด้านขนาน:

ผลต่างของเวกเตอร์สองตัวถูกกำหนดโดยผลรวม: ความแตกต่างของเวกเตอร์และเป็นเวกเตอร์ที่เมื่อรวมกับเวกเตอร์แล้วจะให้เวกเตอร์:

ดังนี้ กฎการหาผลต่างของเวกเตอร์สองตัว: ในการลบเวกเตอร์ออกจากเวกเตอร์ คุณต้องเลื่อนเวกเตอร์เหล่านี้ออกจากจุดหนึ่ง เวกเตอร์ความแตกต่างเชื่อมต่อจุดสิ้นสุดของเวกเตอร์กับจุดสิ้นสุดของเวกเตอร์ (นั่นคือจุดสิ้นสุดของ subtrahend กับจุดสิ้นสุดของ minuend):

การค้นหา มุมระหว่างเวกเตอร์กับเวกเตอร์คุณต้องเลื่อนเวกเตอร์เหล่านี้ออกจากจุดหนึ่ง มุมที่เกิดจากรังสีที่เวกเตอร์วางอยู่เรียกว่ามุมระหว่างเวกเตอร์:

ผลคูณสเกลาร์ของเวกเตอร์สองตัวคือจำนวนที่เท่ากับผลคูณของความยาวของเวกเตอร์เหล่านี้และโคไซน์ของมุมระหว่างเวกเตอร์เหล่านี้:

ฉันขอแนะนำให้คุณแก้ปัญหาจาก Open Task Bank สำหรับ แล้วตรวจสอบวิธีแก้ปัญหาของคุณด้วยวิดีโอสอน:

1 . งาน 4 (หมายเลข 27709)

สองด้านของสี่เหลี่ยมผืนผ้า เอบีซีดีเท่ากับ 6 และ 8 จงหาความยาวของผลต่างของเวกเตอร์ และ

2. งาน 4 (หมายเลข 27710)

สองด้านของสี่เหลี่ยมผืนผ้า เอบีซีดีคือ 6 และ 8 จงหาผลคูณสเกลาร์ของเวกเตอร์ และ (วาดจากงานก่อนหน้า)

3 . งาน 4 (หมายเลข 27711)

สองด้านของสี่เหลี่ยมผืนผ้า เอบีซีดี อ. ค้นหาความยาวของผลรวมของเวกเตอร์และ

4 . งาน 4 (หมายเลข 27712)

สองด้านของสี่เหลี่ยมผืนผ้า เอบีซีดีคือ 6 และ 8 เส้นทแยงมุมตัดกันที่จุด อ. ค้นหาความยาวของผลต่างของเวกเตอร์ และ (วาดจากงานก่อนหน้า)

5 . งาน 4 (หมายเลข 27713)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีคือ 12 และ 16 จงหาความยาวของเวกเตอร์

6. งาน 4 (หมายเลข 27714)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีคือ 12 และ 16 จงหาความยาวของเวกเตอร์ +

7. งาน 4 (หมายเลข 27715)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีคือ 12 และ 16 จงหาความยาวของเวกเตอร์ - .(วาดจากโจทย์ข้อที่แล้ว)

8. งาน 4 (หมายเลข 27716)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีคือ 12 และ 16 จงหาความยาวของเวกเตอร์ -

9 . งาน 4 (หมายเลข 27717)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีตัดกันที่จุด อและเท่ากับ 12 และ 16 จงหาความยาวของเวกเตอร์ +

10 . งาน 4 (หมายเลข 27718)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีตัดกันที่จุด อและเท่ากับ 12 และ 16 ค้นหาความยาวของเวกเตอร์ - .(วาดจากงานก่อนหน้า)

11. งาน 4 (หมายเลข 27719)

เส้นทแยงมุมสี่เหลี่ยมขนมเปียกปูน เอบีซีดีตัดกันที่จุด อและเท่ากับ 12 และ 16 จงหาผลคูณสเกลาร์ของเวกเตอร์ และ . (ดึงมาจากโจทย์ข้อที่แล้ว)

12 . งาน 4 (หมายเลข 27720)

เอบีซีเท่ากัน จงหาความยาวของเวกเตอร์ +

13 . งาน 4 (หมายเลข 27721)

ด้านของสามเหลี่ยมด้านเท่า เอบีซีเท่ากับ 3 ค้นหาความยาวของเวกเตอร์ -. (ภาพวาดจากงานก่อนหน้า)

14 . งาน 4 (หมายเลข 27722)

ด้านของสามเหลี่ยมด้านเท่า เอบีซีเท่ากับ 3 จงหาผลคูณสเกลาร์ของเวกเตอร์ และ (วาดจากงานก่อนหน้า)

เบราว์เซอร์ของคุณอาจไม่รองรับ หากต้องการใช้โปรแกรมจำลอง "Unified State Examination Hour" ให้ลองดาวน์โหลด
ไฟร์ฟอกซ์

คำนิยาม การรวบรวมคำสั่ง (x 1 , x 2 , ... , x n) n ของจำนวนจริงเรียกว่า เวกเตอร์ n มิติ, และตัวเลข x i (i = 1,...,n) - ส่วนประกอบหรือ พิกัด,

ตัวอย่าง. ตัวอย่างเช่น ถ้าโรงงานผลิตรถยนต์แห่งหนึ่งต้องผลิตรถยนต์ 50 คัน รถบรรทุก 100 คัน รถบัส 10 คัน อะไหล่รถยนต์ 50 ชุด และรถบรรทุกและรถโดยสาร 150 ชุดต่อกะ ดังนั้นโปรแกรมการผลิตของโรงงานนี้สามารถเขียนเป็น เวกเตอร์ (50, 100 , 10, 50, 150) ซึ่งมีห้าองค์ประกอบ

สัญกรณ์ เวกเตอร์จะแสดงด้วยอักษรตัวพิมพ์เล็กหรือตัวหนาที่มีแถบหรือลูกศรอยู่ด้านบน ตัวอย่างเช่น กหรือ. เวกเตอร์ทั้งสองเรียกว่า เท่ากันถ้ามีจำนวนส่วนประกอบเท่ากันและส่วนประกอบที่เกี่ยวข้องเท่ากัน

ไม่สามารถแลกเปลี่ยนองค์ประกอบเวกเตอร์ได้ เช่น (3, 2, 5, 0, 1)และ (2, 3, 5, 0, 1) เวกเตอร์ต่างๆ
การดำเนินการกับเวกเตอร์งาน x= (x 1 , x 2 , ... ,x n) เป็นจำนวนจริงλ เรียกว่าเวกเตอร์λ x= (λ x 1 , λ x 2 , ... , λ x n)

ผลรวมx= (x 1 , x 2 , ... ,x n) และ ย= (y 1 , y 2 , ... ,y n) เรียกว่าเวกเตอร์ x+ย= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).

พื้นที่ของเวกเตอร์เอ็น -ปริภูมิเวกเตอร์เชิงมิติ ร n ถูกกำหนดให้เป็นเซตของเวกเตอร์ n มิติทั้งหมดซึ่งกำหนดการดำเนินการของการคูณด้วยจำนวนจริงและการบวก

ภาพประกอบทางเศรษฐกิจ ภาพประกอบทางเศรษฐศาสตร์ของปริภูมิเวกเตอร์ n มิติ: พื้นที่ของสินค้า (สินค้า). ภายใต้ สินค้าเราจะเข้าใจสินค้าหรือบริการบางอย่างที่วางขายในช่วงเวลาหนึ่งในสถานที่หนึ่งๆ สมมติว่ามีสินค้าจำนวนจำกัด n; ปริมาณของสินค้าแต่ละรายการที่ผู้บริโภคซื้อนั้นมีลักษณะเป็นชุดของสินค้า

x= (x 1 , x 2 , ..., x n),

โดยที่ x i หมายถึงจำนวนสินค้าที่ i-th ซื้อโดยผู้บริโภค เราจะถือว่าสินค้าทั้งหมดมีคุณสมบัติในการหารโดยพลการ เพื่อให้สามารถซื้อในปริมาณที่ไม่ติดลบของแต่ละรายการได้ จากนั้นชุดของสินค้าที่เป็นไปได้ทั้งหมดคือเวกเตอร์ของพื้นที่ของสินค้า C = ( x= (x 1 , x 2 , ... , x n) x ผม ≥ 0, ผม = )

ความเป็นอิสระเชิงเส้น ระบบ อี 1 , อี 2 , ... , อี m เวกเตอร์มิติ n เรียกว่า ขึ้นอยู่กับเชิงเส้นหากมีตัวเลขดังกล่าวλ 1 , λ 2 , ... , λ ม ซึ่งอย่างน้อยหนึ่งรายการไม่ใช่ศูนย์ ซึ่งเป็นไปตามความเท่าเทียมกันλ1 อี 1 + λ2 อี 2+...+แลมป์ อีม = 0; มิฉะนั้นจะเรียกระบบเวกเตอร์นี้ว่า อิสระเชิงเส้นนั่นคือความเท่าเทียมกันนี้เป็นไปได้เฉพาะในกรณีที่ทั้งหมด . ความหมายทางเรขาคณิตของการพึ่งพาเชิงเส้นของเวกเตอร์ใน ร 3 , ตีความเป็นส่วนกำกับ, อธิบายทฤษฎีบทต่อไปนี้

ทฤษฎีบท 1. ระบบที่ประกอบด้วยเวกเตอร์ตัวเดียวจะขึ้นอยู่กับเชิงเส้นก็ต่อเมื่อเวกเตอร์นี้เป็นศูนย์

ทฤษฎีบท 2 สำหรับเวกเตอร์สองตัวที่ขึ้นอยู่กับเชิงเส้น มันจำเป็นและเพียงพอที่พวกมันจะต้องเป็นเส้นตรง (ขนานกัน)

ทฤษฎีบท 3 . สำหรับเวกเตอร์สามตัวที่ต้องพึ่งพาเชิงเส้น มันจำเป็นและเพียงพอที่พวกมันจะต้องเป็นระนาบเดียวกัน (อยู่ในระนาบเดียวกัน)

ซ้ายและขวาของเวกเตอร์สามตัว เวกเตอร์สามตัวที่ไม่ใช่ระนาบเดียวกัน ก, ข, คเรียกว่า ขวาถ้าผู้สังเกตจากจุดกำเนิดร่วมกันข้ามจุดสิ้นสุดของเวกเตอร์ ก, ข, คในลำดับนั้นดูเหมือนจะดำเนินไปตามเข็มนาฬิกา มิฉะนั้น ก, ข, ค -ซ้ายสาม. เรียกเวกเตอร์สามเท่าทางขวา (หรือซ้าย) ทั้งหมด อย่างเท่าเทียมกัน มุ่งเน้น

พื้นฐานและพิกัด. ทรอยก้า อี 1, อี 2 , อีเวกเตอร์ที่ไม่ใช่ระนาบร่วม 3 ตัวใน ร 3 โทร พื้นฐานและเวกเตอร์เอง อี 1, อี 2 , อี 3 - ขั้นพื้นฐาน. เวกเตอร์ใดๆ กสามารถขยายได้ในลักษณะเฉพาะในแง่ของเวกเตอร์พื้นฐาน นั่นคือ สามารถแสดงในรูปแบบได้

ก= x 1 อี 1 + x2 อี 2 + x 3 อี 3, (1.1)

หมายเลข x 1 , x 2 , x 3 ในการขยาย (1.1) เรียกว่า พิกัดกเป็นพื้นฐาน อี 1, อี 2 , อี 3 และแสดงเป็น ก(x 1 , x 2 , x 3)

พื้นฐานออร์โธนอร์มัล ถ้าเวกเตอร์ อี 1, อี 2 , อี 3 เป็นคู่ตั้งฉากและความยาวของแต่ละอันเท่ากับหนึ่งจากนั้นจึงเรียกว่าพื้นฐาน ออร์โธนอร์มอล, และพิกัด x 1 , x 2 , x 3 - เป็นรูปสี่เหลี่ยมผืนผ้าเวกเตอร์พื้นฐานของฐานออร์โธนอร์มอลจะแสดงแทน ฉัน, เจ, เค

เราจะถือว่าสิ่งนั้นอยู่ในอวกาศ ร 3 ระบบพิกัดสี่เหลี่ยมคาร์ทีเซียนที่ถูกต้อง (0, ฉัน, เจ, เค}.

สินค้าเวกเตอร์ ศิลปะเวกเตอร์ กต่อเวกเตอร์ ขเรียกว่าเวกเตอร์ คซึ่งถูกกำหนดโดยเงื่อนไขสามประการต่อไปนี้:

1. ความยาวของเวกเตอร์ คตัวเลขเท่ากับพื้นที่ของสี่เหลี่ยมด้านขนานที่สร้างขึ้นบนเวกเตอร์ กและ ขเช่น.
ค= |ก||ข|บาป( ก^ข).

2. เวกเตอร์ คตั้งฉากกับเวกเตอร์แต่ละตัว กและ ข.

3. เวกเตอร์ ก, ขและ ค, ตามลำดับนั้น, สร้างสามตัวที่ถูกต้อง.

สำหรับสินค้าเวกเตอร์ คมีการแนะนำการกำหนด ค=[ab] หรือ
ค = ก × ข.

ถ้าเวกเตอร์ กและ ขเป็นเส้นตรงแล้วบาป ( ก^b) = 0 และ [ ab] = 0 โดยเฉพาะอย่างยิ่ง [ อ่า] = 0. ผลิตภัณฑ์เวกเตอร์ของ orts: [ ไอเจ]=เค [เจเค] = ฉัน, [กี]=เจ.

ถ้าเวกเตอร์ กและ ขให้เป็นพื้นฐาน ฉัน, เจ, เคพิกัด ก(เป็น 1 , เป็น 2 , เป็น 3), ข(ข 1 ข 2 ข 3) แล้ว

งานผสม. ถ้าผลคูณของเวกเตอร์สองตัว กและ ขสเกลาร์คูณด้วยเวกเตอร์ที่สาม ค,จากนั้นจึงเรียกผลคูณของเวกเตอร์สามตัว ผลิตภัณฑ์ผสมและแสดงด้วยสัญลักษณ์ ก พ.ศ.

ถ้าเวกเตอร์ ก ขและ คเป็นพื้นฐาน ฉัน, เจ, เคกำหนดโดยพิกัดของพวกเขา
ก(เป็น 1 , เป็น 2 , เป็น 3), ข(ข 1 ข 2 ข 3) ค(ค 1 , ค 2 , ค 3) แล้ว

ผลิตภัณฑ์ผสมมีการตีความทางเรขาคณิตอย่างง่าย - เป็นสเกลาร์ในค่าสัมบูรณ์เท่ากับปริมาตรของขนานที่สร้างขึ้นจากเวกเตอร์ที่กำหนดสามตัว

ถ้าเวกเตอร์ก่อตัวเป็นสามเท่า แล้วผลคูณของเวกเตอร์นั้นจะเป็นจำนวนบวกเท่ากับปริมาตรที่ระบุ ถ้าสาม ก, ข, ค -ซ้ายแล้ว เอ บี ซี<0 и V = - เอ บี ซีดังนั้น V =|เป็นขค|.

พิกัดของเวกเตอร์ที่พบในปัญหาของบทแรกจะถือว่าสัมพันธ์กับพื้นฐานออร์โทนอร์มอลด้านขวา เวกเตอร์หนึ่งหน่วยมีทิศทางร่วมเป็นเวกเตอร์ เอแสดงด้วยสัญลักษณ์ กอ. เครื่องหมาย ร=โอมแสดงโดยเวกเตอร์รัศมีของจุด M สัญลักษณ์ a, AB หรือ|ก|, | เอบี |โมดูลของเวกเตอร์จะแสดงแทน กและ เอบี

ตัวอย่าง 1.2. หามุมระหว่างเวกเตอร์ ก= 2ม+4นและ ข= ม-น, ที่ไหน มและ n-เวกเตอร์หน่วยและมุมระหว่าง มและ นเท่ากับ 120 o

สารละลาย. เรามี: cos φ = ab/เอบี, เอบี=(2ม+4น) (ม-น) = 2ม 2 - 4น 2 +2นาที=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; ก = ; ก 2 = (2ม+4น) (2ม+4น) =
= 4ม 2 +16นาที+16น 2 = 4+16(-0.5)+16=12 ดังนั้น a = ข= ; ข 2 =
= (ม-น)(ม-น) = ม 2 -2นาที+น 2 = 1-2(-0.5)+1 = 3 ดังนั้น b = ในที่สุดเราก็มี: cosφ \u003d -1/2, φ \u003d 120 o

ตัวอย่าง 1.3รู้จักเวกเตอร์ เอบี(-3,-2.6) และ พ.ศ(-2,4,4), คำนวณความสูง AD ของสามเหลี่ยม ABC

สารละลาย. แสดงพื้นที่ของสามเหลี่ยม ABC โดย S เราได้รับ:
S = 1/2 ก่อนคริสต์ศักราช แล้ว AD=2S/BC, BC== = 6,
ส = 1/2| เอบี ×เอซี |. AC=AB+BCดังนั้นเวกเตอร์ เครื่องปรับอากาศมีพิกัด
.

ก่อนที่คุณจะเรียนรู้ทั้งหมดเกี่ยวกับเวกเตอร์และการดำเนินการกับพวกมัน ปรับแต่งเพื่อแก้ปัญหาง่ายๆ มีเวกเตอร์ขององค์กรของคุณและเวกเตอร์ของความสามารถเชิงนวัตกรรมของคุณ เวกเตอร์ของการเป็นผู้ประกอบการนำคุณไปสู่เป้าหมายที่ 1 และเวกเตอร์ของความสามารถเชิงนวัตกรรม - ไปสู่เป้าหมายที่ 2 กฎของเกมคือคุณไม่สามารถเคลื่อนไปในทิศทางของเวกเตอร์ทั้งสองนี้พร้อมกันและบรรลุเป้าหมายสองอย่างพร้อมกันได้ เวกเตอร์โต้ตอบหรือพูดในทางคณิตศาสตร์ การดำเนินการบางอย่างดำเนินการกับเวกเตอร์ ผลลัพธ์ของการดำเนินการนี้คือเวกเตอร์ "ผลลัพธ์" ซึ่งนำคุณไปสู่เป้าหมายที่ 3

ตอนนี้บอกฉัน: ผลลัพธ์ของการดำเนินการในเวกเตอร์ "องค์กร" และ "ความสามารถเชิงนวัตกรรม" คือเวกเตอร์ "ผลลัพธ์" ถ้าพูดไม่ทันก็อย่าเพิ่งท้อใจ ขณะที่คุณศึกษาบทเรียนนี้ คุณจะสามารถตอบคำถามนี้ได้

ดังที่เราได้เห็นข้างต้น เวกเตอร์จำเป็นต้องมาจากบางจุด กเป็นเส้นตรงถึงจุดหนึ่ง ข. ดังนั้นเวกเตอร์แต่ละตัวจึงไม่เพียงมีค่าตัวเลข - ความยาวเท่านั้น แต่ยังรวมถึงทิศทางทางกายภาพและทางเรขาคณิตด้วย จากนี้เป็นครั้งแรก คำจำกัดความที่ง่ายที่สุดของเวกเตอร์จะได้มา ดังนั้น เวกเตอร์คือส่วนที่ชี้นำจากจุดหนึ่ง กถึงจุด ข. มีการทำเครื่องหมายดังนี้:

และเพื่อเริ่มต้นที่แตกต่างกัน การดำเนินการเวกเตอร์ เราจำเป็นต้องทำความคุ้นเคยกับคำจำกัดความของเวกเตอร์เพิ่มเติม

เวกเตอร์เป็นตัวแทนของจุดที่ต้องไปให้ถึงจากจุดเริ่มต้นบางจุด ตัวอย่างเช่น เวกเตอร์สามมิติมักจะเขียนเป็น (x, y, z) . พูดง่ายๆ ก็คือ ตัวเลขเหล่านี้แสดงถึงระยะทางที่คุณต้องเดินไปในสามทิศทางที่แตกต่างกันเพื่อไปให้ถึงจุดหมาย

ให้เวกเตอร์ได้รับ ในนั้น x = 3 (มือขวาชี้ไปทางขวา) ย = 1 (มือซ้ายชี้ไปข้างหน้า) ซี = 5 (ใต้จุดมีบันไดขึ้น) จากข้อมูลนี้ คุณจะพบจุดโดยการเดิน 3 เมตรในทิศทางที่ระบุโดยมือขวา จากนั้น 1 เมตรในทิศทางที่ระบุโดยมือซ้าย จากนั้นคุณจะพบบันไดรอคุณอยู่ และปีนขึ้นไป 5 เมตร ในที่สุดคุณจะพบ ตัวคุณเองที่จุดสิ้นสุด

ข้อกำหนดอื่นๆ ทั้งหมดเป็นการปรับแต่งคำอธิบายที่นำเสนอข้างต้น ซึ่งจำเป็นสำหรับการดำเนินการต่างๆ บนเวกเตอร์ นั่นคือสำหรับการแก้ปัญหาในทางปฏิบัติ มาดูคำจำกัดความที่เข้มงวดกว่านี้ โดยพิจารณาจากปัญหาเวกเตอร์ทั่วไป

ตัวอย่างทางกายภาพปริมาณเวกเตอร์อาจเป็นการกระจัดของจุดวัสดุที่เคลื่อนที่ในอวกาศ ความเร็วและความเร่งของจุดนี้ ตลอดจนแรงที่กระทำต่อจุดนั้น

เวกเตอร์เรขาคณิตแสดงในพื้นที่สองมิติและสามมิติในแบบฟอร์ม ส่วนกำกับ. นี่คือส่วนที่มีจุดเริ่มต้นและจุดสิ้นสุด

ถ้า กเป็นจุดเริ่มต้นของเวกเตอร์และ ขเป็นจุดสิ้นสุด จากนั้นเวกเตอร์จะแสดงด้วยสัญลักษณ์หรืออักษรตัวพิมพ์เล็กตัวเดียว ในรูป จุดสิ้นสุดของเวกเตอร์จะแสดงด้วยลูกศร (รูปที่ 1)

ความยาว(หรือ โมดูล) ของเวกเตอร์ทางเรขาคณิตคือความยาวของส่วนที่สร้างมันขึ้นมา

เวกเตอร์ทั้งสองเรียกว่า เท่ากัน หากสามารถรวมกันได้ (เมื่อทิศทางตรงกัน) โดยการแปลแบบขนาน เช่น ถ้าขนานกันให้ชี้ไปในทิศทางเดียวกันและยาวเท่ากัน

ในทางฟิสิกส์มักมีการพิจารณา เวกเตอร์ที่ถูกตรึงไว้กำหนดโดยจุดใช้งาน ความยาว และทิศทาง หากจุดของการใช้เวกเตอร์ไม่สำคัญ ก็สามารถถ่ายโอนได้โดยรักษาความยาวและทิศทางไปยังจุดใดๆ ในอวกาศ ในกรณีนี้เรียกว่าเวกเตอร์ ฟรี. เรายินยอมที่จะพิจารณาเท่านั้น เวกเตอร์ฟรี.

การดำเนินการเชิงเส้นบนเวกเตอร์เรขาคณิต

คูณเวกเตอร์ด้วยตัวเลข

สินค้าเวกเตอร์ ต่อหมายเลขเวกเตอร์เรียกว่าเวกเตอร์ที่ได้จากเวกเตอร์โดยการยืด (ที่ ) หรือลดขนาด (ที่ ) ครั้ง และทิศทางของเวกเตอร์จะยังคงอยู่ถ้า และกลับด้านถ้า (รูปที่ 2)

จากนิยามที่ว่าเวกเตอร์และ = จะอยู่บนเส้นเดียวหรือเส้นคู่ขนานกันเสมอ เวกเตอร์ดังกล่าวเรียกว่า คอลิเนียร์. (คุณสามารถพูดได้ว่าเวกเตอร์เหล่านี้ขนานกัน แต่ในพีชคณิตเวกเตอร์เป็นเรื่องปกติที่จะพูดว่า "คอลลิเนียร์") ตรงกันข้ามก็เป็นจริงเช่นกัน: ถ้าเวกเตอร์และคอลลิเนียร์ พวกมันสัมพันธ์กันด้วยความสัมพันธ์

ดังนั้น ความเท่าเทียมกัน (1) จึงแสดงเงื่อนไขของความสอดคล้องกันของเวกเตอร์สองตัว

การบวกและการลบเวกเตอร์

เมื่อเพิ่มเวกเตอร์ คุณจำเป็นต้องรู้สิ่งนั้น ผลรวมเวกเตอร์ และ เรียกว่าเวกเตอร์ที่มีจุดเริ่มต้นตรงกับจุดเริ่มต้นของเวกเตอร์ และจุดสิ้นสุดตรงกับจุดสิ้นสุดของเวกเตอร์ โดยมีเงื่อนไขว่าจุดเริ่มต้นของเวกเตอร์ต่อท้ายเวกเตอร์ (รูปที่ 3)

นิยามนี้สามารถกระจายบนเวกเตอร์จำนวนจำกัดเท่าใดก็ได้ ให้ในช่องว่างที่กำหนด นเวกเตอร์ฟรี เมื่อเพิ่มเวกเตอร์หลายตัว ผลรวมของพวกมันจะถูกใช้เป็นเวกเตอร์ปิด จุดเริ่มต้นนั้นตรงกับจุดเริ่มต้นของเวกเตอร์แรก และสิ้นสุดด้วยจุดสิ้นสุดของเวกเตอร์สุดท้าย นั่นคือ ถ้าจุดเริ่มต้นของเวกเตอร์ต่อท้ายเวกเตอร์ และจุดเริ่มต้นของเวกเตอร์ไปยังจุดสิ้นสุดของเวกเตอร์ เป็นต้น และสุดท้าย ถึงจุดสิ้นสุดของเวกเตอร์ - จุดเริ่มต้นของเวกเตอร์ แล้วผลรวมของเวกเตอร์เหล่านี้คือเวกเตอร์ปิด ซึ่งจุดเริ่มต้นตรงกับจุดเริ่มต้นของเวกเตอร์ตัวแรก และจุดสิ้นสุดของเวกเตอร์นั้นตรงกับจุดสิ้นสุดของเวกเตอร์ตัวสุดท้าย (รูปที่ 4)

คำเหล่านี้เรียกว่าส่วนประกอบของเวกเตอร์ และกฎที่กำหนดขึ้นคือ กฎรูปหลายเหลี่ยม. รูปหลายเหลี่ยมนี้อาจไม่แบน

เมื่อเวกเตอร์คูณด้วยจำนวน -1 จะได้เวกเตอร์ตรงข้าม เวกเตอร์และมีความยาวเท่ากันและมีทิศทางตรงกันข้าม ผลรวมของพวกเขาให้ เวกเตอร์ว่างซึ่งมีความยาวเป็นศูนย์ ไม่ได้กำหนดทิศทางของเวกเตอร์ว่าง

ในพีชคณิตเวกเตอร์ ไม่จำเป็นต้องพิจารณาการดำเนินการลบแยกกัน: การลบเวกเตอร์ออกจากเวกเตอร์หมายถึงการเพิ่มเวกเตอร์ตรงข้ามให้กับเวกเตอร์ เช่น

ตัวอย่างที่ 1ลดความซับซ้อนของนิพจน์:

นั่นคือ เวกเตอร์สามารถเพิ่มและคูณด้วยตัวเลขได้ในลักษณะเดียวกับพหุนาม (โดยเฉพาะอย่างยิ่ง ปัญหาในการทำให้นิพจน์ง่ายขึ้น) โดยปกติแล้ว ความจำเป็นที่จะต้องลดความซับซ้อนของนิพจน์เชิงเส้นที่คล้ายคลึงกันด้วยเวกเตอร์เกิดขึ้นก่อนที่จะคำนวณผลคูณของเวกเตอร์

ตัวอย่างที่ 2เวกเตอร์และทำหน้าที่เป็นเส้นทแยงมุมของสี่เหลี่ยมด้านขนาน ABCD (รูปที่ 4a) แสดงในรูปของ และ เวกเตอร์ , , และ ซึ่งเป็นด้านของสี่เหลี่ยมด้านขนานนี้

สารละลาย. จุดตัดของเส้นทแยงมุมของสี่เหลี่ยมด้านขนานแบ่งครึ่งเส้นทแยงมุมแต่ละเส้น ความยาวของเวกเตอร์ที่ต้องการในเงื่อนไขของปัญหาจะพบได้จากผลบวกครึ่งหนึ่งของเวกเตอร์ที่สร้างรูปสามเหลี่ยมกับเวกเตอร์ที่ต้องการ หรือเป็นครึ่งหนึ่งของความแตกต่าง (ขึ้นอยู่กับทิศทางของเวกเตอร์ที่ทำหน้าที่เป็นเส้นทแยงมุม) หรือ ในกรณีหลัง ให้นำผลรวมครึ่งหนึ่งที่มีเครื่องหมายลบ ผลลัพธ์คือเวกเตอร์ที่ต้องการในเงื่อนไขของปัญหา:

มีเหตุผลทุกประการที่เชื่อได้ว่าตอนนี้คุณตอบคำถามเกี่ยวกับเวกเตอร์ "องค์กร" และ "ความสามารถเชิงนวัตกรรม" อย่างถูกต้องแล้วในตอนต้นของบทเรียนนี้ คำตอบที่ถูกต้อง: เวกเตอร์เหล่านี้อยู่ภายใต้การดำเนินการเพิ่มเติม

แก้ปัญหาเกี่ยวกับเวกเตอร์ด้วยตัวคุณเอง จากนั้นดูวิธีแก้ปัญหา

จะหาความยาวของผลรวมของเวกเตอร์ได้อย่างไร?

ปัญหานี้ใช้พื้นที่พิเศษในการดำเนินการกับเวกเตอร์ เนื่องจากเกี่ยวข้องกับการใช้คุณสมบัติตรีโกณมิติ สมมติว่าคุณมีงานดังต่อไปนี้:

กำหนดความยาวของเวกเตอร์ และความยาวของผลรวมของเวกเตอร์เหล่านี้ ค้นหาความยาวของผลต่างของเวกเตอร์เหล่านี้

วิธีแก้ปัญหานี้และปัญหาอื่นที่คล้ายคลึงกันและคำอธิบายวิธีแก้ปัญหา - ในบทเรียน " การบวกเวกเตอร์: ความยาวของผลรวมของเวกเตอร์และทฤษฎีบทโคไซน์ ".

และสามารถตรวจสอบแนวทางแก้ไขปัญหาดังกล่าวได้ที่ เครื่องคิดเลขออนไลน์ "ด้านที่ไม่รู้จักของสามเหลี่ยม (การบวกเวกเตอร์และทฤษฎีบทโคไซน์)" .

ผลิตภัณฑ์ของเวกเตอร์อยู่ที่ไหน

ผลคูณของเวกเตอร์ต่อเวกเตอร์ไม่ใช่การดำเนินการเชิงเส้นและแยกพิจารณา และเรามีบทเรียน "ดอทโปรดัคของเวกเตอร์" และ "เวกเตอร์และผลคูณของเวกเตอร์"

การฉายเวกเตอร์บนแกน

เส้นโครงของเวกเตอร์บนแกนจะเท่ากับผลคูณของความยาวของเวกเตอร์ที่ฉายและโคไซน์ของมุมระหว่างเวกเตอร์กับแกน:

ดังที่ทราบกันดีว่าเส้นโครงของจุด กบนเส้น (ระนาบ) คือฐานของเส้นตั้งฉากที่ทิ้งจากจุดนี้ไปยังเส้น (ระนาบ)

ให้ - เวกเตอร์โดยพลการ (รูปที่ 5) และ และ - การคาดการณ์ของจุดเริ่มต้น (จุด ก) และจุดสิ้นสุด (จุด ข) ต่อเพลา ล. (เพื่อสร้างเส้นโครงของจุด ก) วาดตรงผ่านจุด กระนาบตั้งฉากกับเส้น จุดตัดของเส้นและระนาบจะเป็นตัวกำหนดการฉายที่ต้องการ

ส่วนประกอบของเวกเตอร์ บนแกน lเรียกว่าเวกเตอร์ที่วางอยู่บนแกนนี้จุดเริ่มต้นที่สอดคล้องกับการฉายของจุดเริ่มต้นและจุดสิ้นสุด - ด้วยการฉายภาพของการสิ้นสุดของเวกเตอร์ .

การฉายภาพเวกเตอร์บนแกน ลโทรหาหมายเลข

เท่ากับความยาวของเวกเตอร์ส่วนประกอบบนแกนนี้ โดยใช้เครื่องหมายบวกถ้าทิศทางของส่วนประกอบตรงกับทิศทางของแกน ลและเครื่องหมายลบหากทิศทางเหล่านี้อยู่ตรงข้ามกัน

คุณสมบัติหลักของเส้นโครงเวกเตอร์บนแกน:

1. เส้นโครงของเวกเตอร์ที่เท่ากันบนแกนเดียวกันมีค่าเท่ากัน

2. เมื่อเวกเตอร์คูณด้วยตัวเลข เส้นโครงของมันจะถูกคูณด้วยจำนวนเดียวกัน

3. เส้นโครงของผลรวมของเวกเตอร์บนแกนใด ๆ จะเท่ากับผลรวมของเส้นโครงบนแกนเดียวกันของพจน์ของเวกเตอร์

4. เส้นโครงของเวกเตอร์บนแกนเท่ากับผลคูณของความยาวของเวกเตอร์ที่ฉายและโคไซน์ของมุมระหว่างเวกเตอร์กับแกน:

สารละลาย. ลองฉายเวกเตอร์บนแกนกัน ลตามที่กำหนดไว้ในการอ้างอิงทางทฤษฎีข้างต้น จากรูปที่ 5a เห็นได้ชัดว่าเส้นโครงของผลรวมของเวกเตอร์เท่ากับผลรวมของเส้นโครงของเวกเตอร์ เราคำนวณประมาณการเหล่านี้:

เราพบเส้นโครงสุดท้ายของผลรวมของเวกเตอร์:

ความสัมพันธ์ของเวกเตอร์กับระบบพิกัดคาร์ทีเซียนสี่เหลี่ยมในอวกาศ

รู้จักกับ ระบบพิกัดคาร์ทีเซียนสี่เหลี่ยมในอวกาศเกิดขึ้นในบทเรียนที่เกี่ยวข้องแนะนำให้เปิดในหน้าต่างใหม่

ในระบบพิกัดของแกนพิกัด 0xyzแกน วัวเรียกว่า แกน xแกน 0 ปี – แกน yและแกน 0z – ใช้แกน.

ด้วยจุดโดยพลการ มเวกเตอร์เน็คไทอวกาศ

เรียกว่า เวกเตอร์รัศมีคะแนน มและฉายไปยังแกนพิกัดแต่ละแกน ให้เราแสดงค่าของการประมาณการที่เกี่ยวข้อง:

ตัวเลข x, y, zเรียกว่า พิกัดจุด Mตามลำดับ แอ๊บซิสซ่า, อุปสมบทและ แอพพลิเคและเขียนเป็นจุดเรียงของตัวเลข: ม(x; y; z)(รูปที่ 6)

เวกเตอร์ของความยาวหน่วยที่มีทิศทางตรงกับทิศทางของแกนเรียกว่า เวกเตอร์หน่วย(หรือ ออร์ต) แกน แสดงโดย

ดังนั้น เวกเตอร์หน่วยของแกนพิกัด วัว, โอ๊ย, ออนซ์

ทฤษฎีบท.เวกเตอร์ใดๆ สามารถแยกย่อยเป็นเวกเตอร์หน่วยของแกนพิกัด:

(2)

ความเท่าเทียมกัน (2) เรียกว่าการขยายตัวของเวกเตอร์ตามแกนพิกัด ค่าสัมประสิทธิ์ของการขยายตัวนี้คือเส้นโครงของเวกเตอร์บนแกนพิกัด ดังนั้น ค่าสัมประสิทธิ์การขยายตัว (2) ของเวกเตอร์ตามแกนพิกัดจึงเป็นพิกัดของเวกเตอร์

หลังจากเลือกระบบพิกัดเฉพาะในอวกาศแล้ว เวกเตอร์และพิกัดสามส่วนจะกำหนดซึ่งกันและกัน ดังนั้นเวกเตอร์จึงสามารถเขียนในรูปแบบ

การแสดงเวกเตอร์ในรูปแบบ (2) และ (3) เหมือนกัน

เงื่อนไขของเวกเตอร์เชิงเส้นตรงในพิกัด

ดังที่เราได้กล่าวไปแล้ว เวกเตอร์จะถูกเรียกว่า collinear หากสัมพันธ์กันโดยความสัมพันธ์

ให้เวกเตอร์ . เวกเตอร์เหล่านี้เป็นเส้นตรงหากพิกัดของเวกเตอร์สัมพันธ์กันโดยความสัมพันธ์

นั่นคือพิกัดของเวกเตอร์เป็นสัดส่วน

ตัวอย่างที่ 6ให้เวกเตอร์ . เวกเตอร์เหล่านี้เป็นเส้นตรงหรือไม่?

สารละลาย. ลองหาอัตราส่วนของพิกัดของเวกเตอร์เหล่านี้กัน:

พิกัดของเวกเตอร์เป็นสัดส่วน ดังนั้น เวกเตอร์จึงเป็นเส้นตรงหรือขนานกัน

โคไซน์ความยาวและทิศทางของเวกเตอร์

เนื่องจากความตั้งฉากร่วมกันของแกนพิกัด ความยาวของเวกเตอร์

เท่ากับความยาวของเส้นทแยงมุมของเส้นขนานสี่เหลี่ยมที่สร้างบนเวกเตอร์

และแสดงออกมาด้วยความเสมอภาค

(4)

เวกเตอร์ถูกกำหนดโดยสมบูรณ์โดยการระบุจุดสองจุด (จุดเริ่มต้นและจุดสิ้นสุด) ดังนั้นพิกัดของเวกเตอร์จึงสามารถแสดงในรูปของพิกัดของจุดเหล่านี้ได้

ให้จุดเริ่มต้นของเวกเตอร์ในระบบพิกัดที่กำหนดอยู่ที่จุด

และจุดสิ้นสุดอยู่ที่จุด

จากความเท่าเทียมกัน

ตามนั้น

หรือในรูปแบบพิกัด

เพราะฉะนั้น, พิกัดของเวกเตอร์จะเท่ากับความแตกต่างของพิกัดที่มีชื่อเดียวกันของจุดสิ้นสุดและจุดเริ่มต้นของเวกเตอร์ . สูตร (4) ในกรณีนี้ใช้แบบฟอร์ม

ทิศทางของเวกเตอร์ถูกกำหนด โคไซน์ทิศทาง . นี่คือโคไซน์ของมุมที่เวกเตอร์ทำกับแกน วัว, โอ๊ยและ ออนซ์. กำหนดมุมเหล่านี้ตามลำดับ α , β และ γ . จากนั้นสามารถหาค่าโคไซน์ของมุมเหล่านี้ได้จากสูตร

โคไซน์ทิศทางของเวกเตอร์ยังเป็นพิกัดของเวกเตอร์และเวกเตอร์ของเวกเตอร์ด้วย