ВЕКТОРИ. ДЕЙСТВИЯПО-ГОРЕВЕКТОРИ. СКАЛАР,

ВЕКТОР, СМЕСЕН ПРОДУКТ ОТ ВЕКТОРИ.

1. ВЕКТОРИ, ДЕЙСТВИЯ ВЪРХУ ВЕКТОРИ.

Основни определения.

Определение 1.Нарича се величина, която се характеризира напълно с числовата си стойност в избраната система от единици скаларенили скаларен .

(Телесно тегло, обем, време и др.)

Определение 2.Нарича се величина, характеризираща се с числена стойност и посока вектор или вектор .

(Изместване, сила, скорост и т.н.)

Обозначения: , или , .

Геометричният вектор е насочен сегмент.

За вектор - точка А- начална точка INе краят на вектора.

Определение 3.Модул вектор е дължината на отсечката AB.

Определение 4.Нарича се вектор, чийто модул е ​​нула нула , е посочено.

Определение 5.Векторите, разположени на успоредни прави или на една и съща права, се наричат колинеарен . Ако два колинеарни вектора имат една и съща посока, тогава те се наричат съпосочен .

Определение 6.Разглеждат се два вектора равен , ако те съвместно режисиран и са равни по модул.

Действия върху вектори.

1) Събиране на вектори.

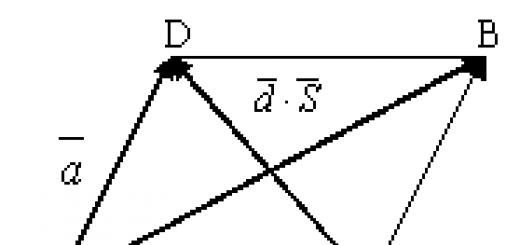
Деф. 6.сума два вектора и е диагоналът на успоредника, изграден върху тези вектори, идващ от обща точка на тяхното приложение (правило на успоредник).

Фиг. 1.

Деф. 7.Сумата от три вектора , , е диагоналът на паралелепипеда, построен върху тези вектори (правило на паралелепипед).

Деф. 8.Ако А, IN, СЪС са произволни точки, тогава + = (правило на триъгълника).

фиг.2

Добавъчни свойства.

1 О . + = + (закон за изместване).

2 О . + ( + ) = ( + ) + = ( + ) + (асоциативен закон).

3 О . + (– ) + .

2) Изваждане на вектори.

Деф. 9.Под разлика вектори и разбирайте вектор = - такива, че + = .

В успоредник това е друго диагонал SD (виж фиг. 1).

3) Умножение на вектор с число.

Деф. 10. работа вектор към скалар к наречен вектор

= к = к ,

дълго ка , и посока, която:

1. съвпада с посоката на вектора ако к > 0;

2. противоположно на посоката на вектора ако к < 0;

3. произволно ако к = 0.

Свойства на умножение на вектор с число.

1 О . (к + л ) = к + л .

к ( + ) = к + к .

2 о . к (л ) = (кл ) .

3 о . 1  = , (–1)  = – , 0  = .

Векторни свойства.

Деф. единадесет.Два вектора и се наричат колинеарен ако се намират на паралелни линииили при една права линия.

Нулевият вектор е колинеарен на всеки вектор.

Теорема 1.Два ненулеви вектора и колинеарен,  когато са пропорционални, т.е.

= к , к - скаларни.

Деф. 12.Три вектора , , се наричат компланарен ако са успоредни на някаква равнина или лежат в нея.

Теорема 2.Три ненулеви вектора , , компланарен,  когато единият от тях е линейна комбинация от другите два, т.е.

= к + л , к , л - скалари.

Проекция на вектор върху ос.

Теорема 3.Проекция на вектор върху ос (насочена линия) ле равно на произведението от дължината на вектора и косинуса на ъгъла между посоката на вектора и посоката на оста, т.е. = а  ° Соперационна система  ,  = ( , л).

2. ВЕКТОРНИ КООРДИНАТИ

Деф. 13.Векторни проекции върху координатни оси о, OU, ОзНаречен векторни координати. Обозначение:  а х , а г , а z .

Дължина на вектора:

Пример:Изчислете дължината на вектора.

Решение:

Разстояние между точките И изчислено по формулата: .

Пример:Намерете разстоянието между точките M (2,3,-1) и K (4,5,2).

Действия върху вектори в координатна форма.

Дадени вектори = а х , а г , а z и = b х , b г , b z .

1. (  )= а х  b х , а г  b г , а z  b z .

2.  =   а х ,  а г ,  а z, където  - скаларни.

Скаларно произведение на вектори.

определение:Под скаларното произведение на два вектора и

се разбира като число, равно на произведението от дължините на тези вектори и косинуса на ъгъла между тях, т.е. = , - ъгъл между векторите и .

Свойства на точков продукт:

1.  =

2. ( + ) =

3.

4.

5. , където са скаларите.

6. два вектора са перпендикулярни (ортогонални), ако .

7. ако и само ако .

Скаларното произведение в координатна форма има формата: , където и .

Пример:Намерете скаларното произведение на вектори и

Решение:

Вектор, държащ вектори.

Определение: Векторното произведение на два вектора и се разбира като вектор, за който:

Модулът е равен на площта на успоредника, изграден върху тези вектори, т.е. , където е ъгълът между векторите и

Този вектор е перпендикулярен на умножените вектори, т.е.

Ако векторите не са колинеарни, тогава те образуват дясна тройка от вектори.

Свойства на кръстосани продукти:

1. При промяна на реда на факторите векторното произведение променя знака си на противоположния, запазвайки модула, т.е.

2 .Векторен квадрат е равен на нулев вектор, т.е.

3 .Скаларният фактор може да бъде изваден от знака на векторното произведение, т.е.

4 .За всеки три вектора, равенството

5 .Необходимо и достатъчно условие за колинеарност на два вектора и :

Векторно произведение в координатна форма.

Ако координатите на векторите и , тогава тяхното векторно произведение се намира по формулата:

.

Тогава от дефиницията на кръстосано произведение следва, че площта на успоредник, изграден върху вектори и се изчислява по формулата:

Пример:Изчислете площта на триъгълник с върхове (1;-1;2), (5;-6;2), (1;3;-1).

Решение: .

Тогава площта на триъгълника ABC ще бъде изчислена, както следва:

,

Смесено произведение на вектори.

определение:Смесено (векторно-скаларно) произведение от вектори е число, определено по формулата: .

Свойства на смесен продукт:

1. Смесеният продукт не се променя при циклична пермутация на неговите фактори, т.е. .

2. При размяна на два съседни фактора смесеното произведение променя знака си на противоположния, т.е. .

3 .Необходимо и достатъчно условие три вектора да са компланарни : =0.

4 .Смесеното произведение на три вектора е равно на обема на паралелепипеда, построен върху тези вектори, взет със знак плюс, ако тези вектори образуват дясна тройка, и със знак минус, ако образуват лява тройка, т.е. .

Ако е известно координативектори , тогава смесеният продукт се намира по формулата:

Пример:Изчислете смесеното произведение на векторите.

Решение:

3. Основа на системата от вектори.

Определение.Система от вектори се разбира като няколко вектора, принадлежащи към едно и също пространство Р.

Коментирайте.Ако системата се състои от краен брой вектори, те се означават с една и съща буква с различни индекси.

Пример.

Определение. Всеки вектор от формата = се нарича линейна комбинация от вектори. Числата са коефициентите на линейната комбинация.

Пример. .

Определение. Ако векторът е линейна комбинация от вектори , тогава казваме, че векторът е линейно изразен чрез векторите .

Определение.Системата от вектори се нарича линейно независими, ако нито един от векторите на системата не може да бъде като линейна комбинация от останалите вектори. В противен случай системата се нарича линейно зависима.

Пример. Векторна система линейно зависими, тъй като векторът .

Дефиниция на основата.Система от вектори формира основа, ако:

1) той е линейно независим,

2) всеки вектор на пространството през него се изразява линейно.

Пример 1Космическа основа: .

2. В системата от вектори векторите са основа: , защото линейно изразено чрез вектори.

Коментирайте.За да намерите основата на дадена система от вектори, трябва да:

1) напишете координатите на векторите в матрицата,

2) използвайки елементарни трансформации, приведете матрицата до триъгълна форма,

3) ненулевите редове на матрицата ще бъдат основата на системата,

4) броят на векторите в базиса е равен на ранга на матрицата.

1. Добавяне. Нека a и b са два вектора. От произволна точка O отделяме вектора OA = a, а от получената точка A - вектора AB = b. OB векторът се нарича сумаа+ bвектори a и b (фиг. 6), а операцията за намиране на сумата от вектори е тяхното събиране.

Нека проверим дали добавянето на вектори е дефинирано правилно, т.е. сумата от векторите не зависи от избора на точка O. За да направите това, вземете всяка друга точка Q и оставете настрана векторите QC = a и CD = b. Тъй като QC = OA = a, по критерия за равенство на два вектора (1.8) получаваме, че OQ = AC. По същия начин от равенството AB = CD = b следва, че AC = BD. Следователно OQ = BD и, отново прилагайки критерия (1.8), получаваме OB = QD, което трябваше да бъде доказано (фиг. 7).

Правилото на триъгълника следва директно от дефиницията на сумата от два вектора:

(2.1) за всякакви три точки O, A и B OA + AB = OB.

Освен това, както е известно от училищния курс по геометрия, за всякакви три точки O, A и B дължината на отсечката OB не надвишава сумата от дължините на отсечките OA и AB и равенството |OB| = |OA| + |AB| се достига само когато точка А лежи на отсечката [OB]. Това неравенство често се нарича неравенство на триъгълника. Дефиницията на сумата от вектори ви позволява да я запишете във векторна форма:

(2.2) |а + b| |а| + |b| .

Равенство в (2.2) се постига тогава и само тогава, когато векторите a и b са в една и съща посока, а в останалите случаи неравенството е строго. Запишете равенството |a+b| = |a|+|b| за произволни вектори - груба грешка.

2. Основни свойства на векторното събиране. Те включват:

(C1) За всеки три вектора a, b и c (a+b)+c = a+(b+c) (асоциативност).

(С2) За всеки два вектора a и b a+b = b+a (комутативност).

(С3) За произволен вектор a a+0 = a.

(C4) За всеки две точки A и B AB + BA = 0.

IN

С оглед на последното свойство векторите BA и AB се наричат ​​противоположни. Векторът, противоположен на вектора a, се означава с "-a".



Свойства (C3) и (C4) следват директно от правилото на триъгълника (проверете!). За да докажем (C2), от произволна точка O отделяме векторите OA = a и OS = b, а от точка A - вектора AB = b (фиг. 8). Тъй като OS \u003d AB, чрез знака за равенство на два насочени сегмента, получаваме, че OA \u003d CB. Но OA \u003d a, следователно също CB = а. Забележете сега, че според правилото на триъгълника векторът OB може да бъде представен както като OA + OB = a + b, така и като OC + CB = b + a. Оказва се, че a + b = b + a = OS, което трябваше да се докаже.

Нека докажем свойството (С1). За да направим това, ние последователно отлагаме векторите OA = a, AB = b и BC = c. По дефиницията на векторно събиране, (a + b) + c = OB + BC и a + (b + c) = OA + AC. Но OB + BC \u003d OA + AC \u003d OS (фиг. 9).

Обърнете внимание, че на фиг. 8OC = AB. Следователно е справедливо

(2.3) Правило на успоредник: Сумата от неколинеарни вектори a и b е равна на диагонала OB на успоредника OABS, построен върху векторите 2 OA = a и OS = b.

В допълнение, от горното доказателство за асоциативност, получаваме

(2.4) Правило на многоъгълника. За да добавите няколко вектора, взети в определен ред, трябва да ги оставите един след друг, така че краят на всеки вектор да служи като начало на следващия, и след това да свържете началото на първия с края на последния.

Доказахме това правило само за случая на три вектора, но горното разсъждение може лесно да се разшири до произволен брой членове.

П

Тъй като началото на нулевия насочен сегмент съвпада с края, полезен резултат следва от правилото на многоъгълника.

(2.5) Правило за затворена верига. Сумата от няколко вектора е равна на нула тогава и само ако, когато са последователно отложени, те образуват затворена верига, т.е. краят на последния съвпада с началото на първия.

(2.6) Упражнение. Докажете правилото на паралелепипеда: за да добавите три вектора, които не са успоредни на една и съща равнина, трябва да ги отделите от една точка O, да завършите трите получени сегмента до паралелепипед и да начертаете диагонал на този паралелепипед от точка O, което ще бъде желаната сума (фиг. 10).

Асоциативността на събирането на вектори показва, че сумата от три вектора, взети в определен ред, не зависи от това дали първо добавяме първите два вектора и след това третия към тях, или първо намираме сумата от втория и третия вектори и след това го добавете към първия . Това означава, че можем да запишем сумата от три вектора като a + b + c, без да мислим как да поставим скоби в нея. В курса по алгебра ще бъде показано, че ако това свойство е валидно за три термина, тогава то е валидно за произволен брой от тях, тоест можем да запишем произволна векторна сума a + b + c + ... + без да се притесняваме за начина, по който са поставени скобите d. И свойството комутативност (C2) показва, че можем също, без да променяме тази сума, произволно да пренаредим членовете в нея. Това е значението на асоциативността и комутативността.

3

. Изваждане на вектори. Разликата a–b на векторите a и b е вектор x, такъв че x+b = a. Операцията за намиране на разликата на векторите се нарича тяхното изваждане.

Нека отделим векторите OA=a и OB=b от произволна точка O. Очевидно единственият вектор, който заедно с OB дава OA, е векторът BA. По този начин,

(2.7) всеки два вектора имат разлика и то само един. За да го изградите, трябва да отложите векторите от една точка и да свържете края на втория с края на първия (фиг. 11).

З

Също така отбелязваме, че на фиг. 11 VA = BO + OA. Означава, че

a–b = a+(–b).

С други думи, изваждането на един вектор от друг е като добавяне на първия вектор към противоположния вектор на втория.

Нека векторите a и b не са колинеарни. Тогава точките O, A и B образуват триъгълник. Ако го завършим до успоредника OASV, тогава диагоналът в него
ще представлява сумата a + b и диагоналът
- разлика a-b (фиг. 12). Това е полезно допълнение към правилото на успоредника.

Равенството (2.8) може да се докаже и чисто алгебрично. Наистина, ако x = a+(–b) , тогава x+b = a+(–b)+b = a+0 = а. Може също да се покаже алгебрично, че разликата a–b няма други стойности: x+b = а (x+b)+(–b) = a+(–b) x+(b+(–b)) = a+(–b) x+0=a+(–b) x = a+(–b). Умишлено записахме всички тези трансформации в детайли, за да покажем, че всички те разчитат само на основните свойства на събирането (C1)-(C4) (проверете!). В общата теория на векторните пространства, за която ще научите в курса си по алгебра, тези свойства се приемат като аксиоми на векторното събиране и всички други свойства на събирането се извличат от тях.

4. Умножение на вектор с число. Умножаването на вектор по число е операция за намиране на произведението на вектор по число. Произведението на ненулев вектор a и число x е вектор, обозначен с "xa" и удовлетворява следните две условия:

(P1) | ха | = |x||a| ; (P2) ха и ако x 0 и ха и ако x<0.

Произведението на нулев вектор с произволно число по дефиниция е равно на 0.

Условието (A1) остава валидно зах= 0, но условие (A2) в този случай е нарушено при x<0 (из-за чего случай нулевого вектора и приходится рассматривать отдельно). Однако, при любых а и х векторы а и ха коллинеарны (почему?).

Обърнете внимание, че xa = 0 |ха| = 0  |x||a| = 0  |x| = 0 или |a| = 0  х = 0 или а = 0. И така,

(2.9) Произведението на вектор и число е равно на нула тогава и само ако числото или векторът са равни на нула.

Нека са дадени ненулево число x и вектор a. От произволна точка O отделяме вектора OA = a и се опитваме да построим векторОХ= ха. Тъй като векторите a и xa трябва да са колинеарни, сегментът
трябва да лежи на правата (OA), а дължината му, съгласно условие (A1), трябва да бъде равна на |x||a|. Има точно два такива сегмента и един от тях (да го наречем
) е режисиран съвместно с
, а другият (да го наречем
) е насочен противоположно
(фиг. 13). Връщайки се към условие (P2), виждаме това
=
за x > 0 и
=
при х< 0.

T

Така всеки вектор може да бъде умножен по произволно число и резултатът е еднозначно определен.

Основните свойства на умножението на вектори с числа включват следното:

(Y1) За всеки вектор a 1a=a (т.е. умножението по 1 не променя вектора).

(Y2) За всякакви числа x, y и вектор a x(ya) = (xy)a (асоциативност).

(Y3) За всякакви числа x, y и вектор a (x + y) a = xa + ya (разпределимост на умножението по отношение на събирането на числа).

(Y4) За всяко число x и вектори a и b x(a + b) = xa + xb (разпределимост на умножението по отношение на събирането на вектори).

Първото от тези свойства следва директно от дефиницията (проверете!). Доказателствата за останалото могат да бъдат намерени на страници 14-16 от L.S. Атанасян и В.Т. Базилев "Геометрия" (част 1).

Също така отбелязваме следните свойства на умножение на вектор с число:

(2.10) Ако векторът a е различен от нула, тогава a/|a| е единичният вектор, съпосочен с вектор a. 3

 Действително, векторите a и a/|a| са еднопосочни (защото 1/|a| > 0) и |a/|a|| = |a|/|a| = 1.

(2.11) (–1)а = –а.

 Действително, по дефиницията за умножаване на вектор по число, векторите (–1)a и a са противоположно насочени и техните дължини са равни.

5. Признаци на колинеарност.

(2.12) Критерий вектор да бъде колинеарен на ненулев вектор. Векторът b е колинеарен на ненулевия вектор a тогава и само ако съществува такова числоT, че b =TА. Освен това, ако векторите a и b са еднопосочни, тогава t = |b| / |a|, а ако са противоположно насочени, то t = – |b| / |a|.

 Вече отбелязахме, че векторите a и ta винаги са колинеарни. Обратно, вземете ненулев вектор a и колинеарен вектор b. Ако са съпосочни, тогава поставяме t = |b|/|a|. След това |ta| = |t||а| = (|b|/|a|)|a| = |b| и векторът ta е сънасочен с a и следователно с b. Следователно, та = b съгласно характеристика 1.7. Ако b, задаваме t = –|b|/|a|. И отново |ta| = |t||а| = (|b|/|a|)|a| = |b|, докато векторите ta и b, насочени противоположно на вектора a, са съпосочни съгласно (Н5). Следователно, в този случай, та = b.

Предупреждението, че векторът a е различен от нула, понякога е неудобно. Тогава можете да използвате това

(2.13) Знак за колинеарност на два вектора. Два вектора са колинеарни тогава и само ако единият от тях може да бъде изразен чрез другия чрез умножаване по число.

 За случая, когато поне един от двата дадени вектора не е равен на нула, това беше доказано по-горе. Ако и двата вектора са нула, тогава, първо, те са колинеарни и, второ, всеки от тях може да бъде получен от другия чрез умножаване по произволно число, така че в този случай всичко е наред.

6. Запазване на паралелизма при операции върху вектори.

(2.14) Лема за паралелизма. Ако два вектора са успоредни на някаква права (равнина), то същата права (равнина) е успоредна на тяхната сума. Ако векторът е успореден на права (равнина), тогава същата права (равнина) е успоредна на произведението си с произволно число.

 Нека векторите a и b са успоредни на дадената права (равнина). Нека отделим от произволната му точка O векторите OA = a и AB = b. Тогава точки A и B също ще лежат на тази права (равнина). Това означава, че там ще лежи и отсечката OB, представляваща сбора a + b, което означава, че е успоредна на тази права (равнина).

Нека сега вземем произволно число x и отделим вектора OS = xa от същата точка O. Ако a \u003d 0, тогава xa \u003d 0 и нулевият вектор е успореден на всяка права и равнина. Ако не, тогава сегментът OS, представляващ вектора xa, ще лежи изцяло на правата линия OA и следователно на дадената права линия (равнина). Така векторът xa ще бъде успореден на тази права (равнина).

Вектори. Действия с вектори. В тази статия ще говорим за това какво е вектор, как да намерим неговата дължина и как да умножим вектор по число, както и как да намерим сбора, разликата и точковия продукт на два вектора.

Както обикновено, малко от най-необходимата теория.

Векторът е насочен сегмент, т.е. сегмент, който има начало и край:

Тук точка А е началото на вектора, а точка В е неговият край.

Векторът има два параметъра: неговата дължина и неговата посока.

Дължината на вектора е дължината на сегмента, свързващ началото и края на вектора. Означава се дължината на вектор

Два вектора се наричат ​​равниако имат еднаква дължина и са подравнени.

Двата вектора се наричат съпосочен, ако лежат на успоредни прави и са насочени в една и съща посока: векторите и са сънасочени:

Два вектора се наричат ​​противоположно насочени, ако лежат на успоредни прави и са насочени в противоположни посоки: векторите и , както и и са насочени в противоположни посоки:

Векторите, лежащи на успоредни прави, се наричат ​​колинеарни: векторите , и са колинеарни.

Векторен продуктчислото се нарича вектор, ко-насочен към вектора if title="k>0">, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :!}

Да се добавете два вектораи трябва да свържете началото на вектора с края на вектора. Сумиращият вектор свързва началото на вектора с края на вектора:

Това правило за добавяне на вектори се нарича правило на триъгълника.

За да добавите два вектора правило на успоредник, трябва да отложите вектора от една точка и да го завършите до успоредник. Сумиращият вектор свързва началото на векторите с противоположния ъгъл на успоредника:

Разлика на два векторасе определя чрез сумата: разликата на векторите и е такъв вектор, който в сумата с вектора ще даде вектор:

Оттук следва правило за намиране на разликата на два вектора: за да извадите вектор от вектор, трябва да отложите тези вектори от една точка. Векторът на разликата свързва края на вектора с края на вектора (т.е. края на субтрахенда с края на умаляваното):

Да намеря ъгъл между вектор и вектор, трябва да отложите тези вектори от една точка. Ъгълът, образуван от лъчите, върху които лежат векторите, се нарича ъгъл между векторите:

Скаларното произведение на два вектора е число, равно на произведението на дължините на тези вектори и косинуса на ъгъла между тях:

Предлагам ви да решите задачи от Open Task Bank за и след това проверете решението си с ВИДЕО УРОЦИ:

1 . Задача 4 (№ 27709)

Две страни на правоъгълник ABCDса равни на 6 и 8. Намерете дължината на разликата на векторите и .

2. Задача 4 (№ 27710)

Две страни на правоъгълник ABCDса 6 и 8. Намерете скаларното произведение на векторите и . (рисунка от предната задача).

3 . Задача 4 (№ 27711)

Две страни на правоъгълник ABCD О. Намерете дължината на сумата от вектори и .

4 . Задача 4 (№ 27712)

Две страни на правоъгълник ABCDса 6 и 8. Диагоналите се пресичат в точката О. Намерете дължината на разликата на векторите и . (рисунка от предната задача).

5. Задача 4 (№ 27713)

Диагонали на ромб ABCDса 12 и 16. Намерете дължината на вектора .

6. Задача 4 (№ 27714)

Диагонали на ромб ABCDса 12 и 16. Намерете дължината на вектора + .

7. Задача 4 (№ 27715)

Диагонали на ромб ABCDса 12 и 16. Намерете дължината на вектора - .(чертайте от предишната задача).

8. Задача 4 (№ 27716)

Диагонали на ромб ABCDса 12 и 16. Намерете дължината на вектора - .

9. Задача 4 (№ 27717)

Диагонали на ромб ABCDпресичат се в точка Ои са равни на 12 и 16. Намерете дължината на вектора + .

10. Задача 4 (№ 27718)

Диагонали на ромб ABCDпресичат се в точка Ои са равни на 12 и 16. Намерете дължината на вектора - .(чертеж от предната задача).

11. Задача 4 (№ 27719)

Диагонали на ромб ABCDпресичат се в точка Ои са равни на 12 и 16. Намерете скаларното произведение на векторите и .(чертайки от предишната задача).

12 . Задача 4 (№ 27720)

ABCравен Намерете дължината на вектора +.

13 . Задача 4 (№ 27721)

Страни на равностранен триъгълник ABCса равни на 3. Намерете дължината на вектора -.(чертежа от предната задача).

14 . Задача 4 (№ 27722)

Страни на равностранен триъгълник ABCса равни на 3. Намерете скаларното произведение на векторите и . (рисунка от предната задача).

Вероятно вашият браузър не се поддържа. За да използвате симулатора „Час за единен държавен изпит“, опитайте да изтеглите
Firefox

Определение Подредена колекция (x 1 , x 2 , ... , x n) n от реални числа се нарича n-мерен вектор, и числата x i (i = 1,...,n) - компонентиили координати,

Пример. Ако например даден автомобилен завод трябва да произведе 50 автомобила, 100 камиона, 10 автобуса, 50 комплекта резервни части за автомобили и 150 комплекта за камиони и автобуси на смяна, тогава производствената програма на този завод може да се напише като вектор (50, 100, 10, 50, 150), който има пет компонента.

Нотация. Векторите се обозначават с удебелени малки букви или букви с лента или стрелка в горната част, например, аили. Двата вектора се наричат равенако имат еднакъв брой компоненти и съответните им компоненти са равни.

Векторните компоненти не могат да се разменят, например (3, 2, 5, 0, 1)и (2, 3, 5, 0, 1) различни вектори.
Операции с вектори.работа х= (x 1 , x 2 , ... ,x n) към реално числоλ наречен векторλ х= (λ x 1, λ x 2, ..., λ x n).

сумах= (x 1 , x 2 , ... ,x n) и г= (y 1 , y 2 , ... ,y n) се нарича вектор x+y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Пространството на векторите.н -дименсионално векторно пространство Р n се дефинира като набор от всички n-мерни вектори, за които са дефинирани операциите умножение с реални числа и събиране.

Икономическа илюстрация. Икономическа илюстрация на n-мерно векторно пространство: пространство на стоките (стоки). Под стокаще разбираме някаква стока или услуга, която е пусната в продажба в определено време на определено място. Да приемем, че има краен брой налични стоки n; количествата на всеки от тях, закупени от потребителя, се характеризират с набор от стоки

х= (x 1, x 2, ..., x n),

където x i означава количеството на i-тата стока, закупена от потребителя. Ще приемем, че всички стоки имат свойството на произволна делимост, така че всяко неотрицателно количество от всяка от тях може да бъде купено. Тогава всички възможни набори от стоки са вектори на пространството от стоки C = ( х= (x 1, x 2, ..., x n) x i ≥ 0, i = ).

Линейна независимост. Система д 1 , д 2 , ... , д m n-мерни вектори се нарича линейно зависимиако има такива числаλ 1 , λ 2 , ... , λ m , от които поне една е различна от нула, което удовлетворява равенствотоλ1 д 1 + λ2 д 2+...+λm д m = 0; иначе тази система от вектори се нарича линейно независими, тоест това равенство е възможно само в случай, когато всички . Геометричният смисъл на линейната зависимост на векторите в Р 3, интерпретирани като насочени отсечки, обясняват следните теореми.

Теорема 1. Система, състояща се от един вектор, е линейно зависима тогава и само ако този вектор е нула.

Теорема 2. За да бъдат два вектора линейно зависими е необходимо и достатъчно те да са колинеарни (успоредни).

Теорема 3 . За да бъдат линейно зависими три вектора, е необходимо и достатъчно те да са копланарни (да лежат в една равнина).

Лява и дясна тройка вектори. Тройка некомпланарни вектори a, b, cНаречен точно, ако наблюдателят от общия им произход заобикаля краищата на векторите a, b, cв този ред изглежда, че продължава по часовниковата стрелка. В противен случай a, b, c -лява тройка. Всички десни (или леви) тройки вектори се наричат по равно ориентиран.

Основа и координати. Тройка д 1, д 2 , д 3 некомпланарни вектора в Р 3 се обадих база, и самите вектори д 1, д 2 , д 3 - основен. Всеки вектор аможе да бъде разширено по уникален начин по отношение на базисни вектори, т.е. може да бъде представено във формата

А= x 1 д 1 + x2 д 2 + х 3 д 3, (1.1)

се наричат ​​числата x 1 , x 2 , x 3 в разширението (1.1). координатиав основата д 1, д 2 , д 3 и са означени а(x 1, x 2, x 3).

Ортонормална основа. Ако векторите д 1, д 2 , д 3 са по двойки перпендикулярни и дължината на всеки от тях е равна на единица, тогава основата се нарича ортонормална, и координатите x 1 , x 2 , x 3 - правоъгълен.Ще бъдат означени базисните вектори на ортонормална база i, j, k.

Ще приемем, че в космоса Р 3 дясната система от декартови правоъгълни координати (0, i, j, k}.

Векторен продукт. векторно изкуство Ана вектор bнаречен вектор ° С, което се определя от следните три условия:

1. Дължина на вектора ° Счислено равна на площта на успоредника, изграден върху векторите аИ б,т.е.
° С= |a||b|грях( а^b).

2. Вектор ° Сперпендикулярно на всеки от векторите аИ b.

3. Вектори а, bИ ° С, взети в този ред, образуват дясна тройка.

За векторен продукт ° Ссе въвежда обозначението c=[аб] или
c = a × b.

Ако векторите аИ bса колинеарни, тогава sin( a^b) = 0 и [ аб] = 0, по-специално, [ аа] = 0. Векторни произведения на orts: [ ij]=к, [jk] = аз, [ki]=й.

Ако векторите аИ bдадено в основата i, j, kкоординати а(a 1, a 2, a 3), b(b 1 , b 2 , b 3), тогава

Смесена работа. Ако кръстосаното произведение на два вектора АИ bскалар, умножен по третия вектор ° С,тогава се нарича такова произведение на три вектора смесен продукти се обозначава със символа а пр.н.е.

Ако векторите а, бИ ° Св основата i, j, kопределени от техните координати
а(a 1, a 2, a 3), b(b 1, b 2, b 3), ° С(c 1 , c 2 , c 3), тогава

.

Смесеният продукт има проста геометрична интерпретация - той е скалар, по абсолютна стойност равен на обема на паралелепипед, изграден върху три дадени вектора.

Ако векторите образуват дясна тройка, тогава тяхното смесено произведение е положително число, равно на посочения обем; ако тримата а, б, в -наляво, тогава a b c<0 и V = - a b c, следователно V =|a b c|.

Приема се, че координатите на векторите, срещани в задачите от първа глава, са дадени спрямо дясната ортонормална основа. Единичен вектор, съпосочен на вектор а,обозначен със символа АО. Символ r=ОМозначени с радиус вектора на точката M, символите a, AB или|а|, | AB |модулите на векторите са означени АИ AB.

Пример 1.2. Намерете ъгъла между векторите а= 2м+4нИ b= м-н, Където мИ н-единични вектори и ъгъл между тях мИ нравен на 120 o.

Решение. Имаме: cos φ = аб/ab, ab=(2м+4н) (м-н) = 2м 2 - 4н 2 +2мн=
= 2 - 4+2cos120 o = - 2 + 2(-0,5) = -3; а = ; а 2 = (2м+4н) (2м+4н) =
= 4м 2 +16мн+16н 2 = 4+16(-0,5)+16=12, така че a = . b= ; b 2 =
= (m-n)(м-н) = м 2 -2мн+н 2 = 1-2(-0,5)+1 = 3, така че b = . Накрая имаме: cosφ \u003d -1/2, φ \u003d 120 o.

Пример 1.3.Познаване на вектори AB(-3, -2,6) и пр.н.е(-2,4,4), изчислете височината AD на триъгълник ABC.

Решение. Означавайки площта на триъгълника ABC с S, получаваме:
S = 1/2 пр.н.е. Тогава AD=2S/BC, BC== = 6,
S = 1/2| AB ×AC |. AC=AB+BC, така че векторът ACима координати
.

Преди да научите всичко за векторите и операциите върху тях, настройте се за решаване на проста задача. Има вектор на вашето предприятие и вектор на вашите иновативни способности. Векторът на предприемачеството ви води към цел 1, а векторът на иновативните способности - към цел 2. Правилата на играта са такива, че не можете да се движите в посоките на тези два вектора едновременно и да постигнете две цели наведнъж. Векторите взаимодействат или, казано математически, върху векторите се извършва някаква операция. Резултатът от тази операция е векторът "Резултат", който ви води до Цел 3.

Сега ми кажете: резултатът от коя операция върху векторите "Предприятие" и "Иновационни способности" е векторът "Резултат"? Ако не можете да кажете веднага, не се обезсърчавайте. Докато изучавате този урок, ще можете да отговорите на този въпрос.

Както видяхме по-горе, векторът задължително идва от някаква точка Апо права линия до някаква точка б. Следователно всеки вектор има не само числова стойност - дължина, но и физическа и геометрична - посока. От това се извлича първата, най-проста дефиниция на вектор. И така, векторът е насочен сегмент, излизащ от точка Акъм основния въпрос б. Маркира се така:

И да започне различно векторни операции , трябва да се запознаем с още една дефиниция на вектор.

Векторът е вид представяне на точка, която трябва да бъде достигната от някаква начална точка. Например, триизмерен вектор обикновено се записва като (x, y, z) . Просто казано, тези числа показват колко далеч трябва да отидете в три различни посоки, за да стигнете до точката.

Нека е даден вектор. При което х = 3 (дясната ръка сочи надясно) г = 1 (лявата ръка сочи напред) z = 5 (под точката има стълба, водеща нагоре). От тези данни ще намерите точката, като вървите 3 метра в посоката, посочена от дясната ръка, след това 1 метър в посоката, посочена от лявата ръка, а след това ви очаква стълба и изкачвайки се 5 метра, накрая ще намерите себе си в крайната точка.

Всички други термини са уточнения на обяснението, представено по-горе, необходими за различни операции върху вектори, тоест за решаване на практически проблеми. Нека преминем през тези по-строги дефиниции, като се спрем на типичните векторни проблеми.

Физически примеривекторни величини могат да бъдат преместването на материална точка, движеща се в пространството, скоростта и ускорението на тази точка, както и силата, действаща върху нея.

геометричен векторпредставени в двумерно и тримерно пространство във формата насочен сегмент. Това е сегмент, който има начало и край.

Ако Ае началото на вектора и бе неговият край, тогава векторът се означава със символа или с една малка буква . На фигурата краят на вектора е обозначен със стрелка (фиг. 1)

Дължина(или модул) на геометричен вектор е дължината на сегмента, който го генерира

Двата вектора се наричат равен , ако могат да се комбинират (когато посоките съвпадат) чрез паралелен превод, т.е. ако са успоредни, сочат в една посока и имат равни дължини.

Във физиката често се разглежда фиксирани вектори, дадени от точката на приложение, дължината и посоката. Ако точката на приложение на вектора няма значение, тогава той може да бъде прехвърлен, запазвайки дължината и посоката към всяка точка в пространството. В този случай векторът се нарича Безплатно. Съгласни сме да разгледаме само безплатни вектори.

Линейни операции върху геометрични вектори

Умножете вектор по число

Векторен продукт на бройВектор се нарича вектор, получен от вектор чрез разтягане (при ) или свиване (при ) пъти и посоката на вектора се запазва, ако , и се обръща, ако . (фиг. 2)

От определението следва, че векторите и = винаги са разположени на една или успоредни прави. Такива вектори се наричат колинеарен. (Можете също така да кажете, че тези вектори са успоредни, но във векторната алгебра е обичайно да се казва „колинеарни“.) Обратното също е вярно: ако векторите и са колинеарни, тогава те са свързани с връзката

Следователно равенството (1) изразява условието за колинеарност на два вектора.

Векторно събиране и изваждане

Когато добавяте вектори, трябва да знаете това сумавектори и се нарича вектор, чието начало съвпада с началото на вектора, а краят съвпада с края на вектора, при условие че началото на вектора е прикрепено към края на вектора. (фиг. 3)

Тази дефиниция може да бъде разпределена върху произволен краен брой вектори. Нека в даденото пространство нбезплатни вектори. При добавяне на няколко вектора тяхната сума се приема като затварящ вектор, чието начало съвпада с началото на първия вектор, а краят с края на последния вектор. Тоест, ако началото на вектора е прикрепено към края на вектора, а началото на вектора към края на вектора и т.н. и накрая до края на вектора - началото на вектора, тогава сумата от тези вектори е затварящият вектор , чието начало съвпада с началото на първия вектор , а краят съвпада с края на последния вектор . (фиг. 4)

Членовете се наричат ​​компоненти на вектора, а формулираното правило е правило на многоъгълника. Този многоъгълник може да не е плосък.

Когато един вектор се умножи по числото -1, се получава противоположният вектор. Векторите и имат еднаква дължина и противоположни посоки. Сборът им дава нулев вектор, чиято дължина е нула. Посоката на нулевия вектор не е дефинирана.

Във векторната алгебра няма нужда да разглеждаме операцията на изваждане отделно: да извадим вектор от вектор означава да добавим срещуположния вектор към вектора, т.е.

Пример 1Опростете израза:

.

,

тоест векторите могат да се добавят и умножават по числа по същия начин като полиномите (по-специално, също и проблеми за опростяване на изрази). Обикновено възниква необходимостта от опростяване на линейно подобни изрази с вектори, преди да се изчислят продуктите на векторите.

Пример 2Векторите и служат като диагонали на успоредника ABCD (фиг. 4а). Изразете по отношение на и векторите , , и , които са страните на този успоредник.

Решение. Пресечната точка на диагоналите на успоредника разполовява всеки диагонал. Дължините на векторите, необходими в условието на задачата, се намират или като половината от сумите на векторите, които образуват триъгълник с желаните, или като половината от разликите (в зависимост от посоката на вектора, служещ за диагонал), или, както в последния случай, половината от сумата, взета със знак минус. Резултатът са векторите, необходими в условието на проблема:

Има всички основания да вярваме, че вече сте отговорили правилно на въпроса за векторите „Предприятие“ и „Иновативни способности“ в началото на този урок. Правилен отговор: тези вектори са подложени на операция на добавяне.

Решете сами задачи върху вектори и след това разгледайте решенията

Как да намерим дължината на сумата от вектори?

Тази задача заема специално място в операциите с вектори, тъй като включва използването на тригонометрични свойства. Да приемем, че имате задача като следната:

Като се има предвид дължината на векторите и дължината на сумата от тези вектори. Намерете дължината на разликата на тези вектори.

Решения на този и други подобни проблеми и обяснения как да ги разрешите - в урока " Векторно събиране: дължината на сумата от вектори и косинусовата теорема ".

И можете да проверите решението на такива проблеми на Онлайн калкулатор "Неизвестна страна на триъгълник (векторно събиране и косинусова теорема)" .

Къде са продуктите на векторите?

Продуктите от вектор по вектор не са линейни операции и се разглеждат отделно. И имаме уроци „Точково произведение на вектори“ и „Векторно и смесено произведение на вектори“.

Проекция на вектор върху ос

Проекцията на вектор върху ос е равна на произведението на дължината на проектирания вектор и косинуса на ъгъла между вектора и оста:

Както е известно, проекцията на точка Ана правата (равнината) е основата на перпендикуляра, пуснат от тази точка на правата (равнината).

Нека - произволен вектор (фиг. 5), и и - проекции на неговото начало (точки А) и край (точки б) на ос л. (За изграждане на проекцията на точка А) начертайте направо през точката Аравнина, перпендикулярна на правата. Пресечната точка на права и равнина ще определи необходимата проекция.

Компонент на вектора по оста lнаричаме такъв вектор, лежащ на тази ос, чието начало съвпада с проекцията на началото, а краят - с проекцията на края на вектора .

Проекцията на вектора върху оста лнарече номер

,

равна на дължината на компонентния вектор на тази ос, взета със знак плюс, ако посоката на компонента съвпада с посоката на оста л, и със знак минус, ако тези посоки са противоположни.

Основните свойства на векторните проекции върху оста:

1. Проекциите на еднакви вектори върху една и съща ос са равни една на друга.

2. Когато един вектор се умножи по число, неговата проекция се умножи по същото число.

3. Проекцията на сумата от вектори върху всяка ос е равна на сумата от проекциите върху същата ос на членовете на векторите.

4. Проекцията на вектор върху ос е равна на произведението на дължината на проектирания вектор и косинуса на ъгъла между вектора и оста:

.

Решение. Нека проектираме векторите върху оста лкакто е дефинирано в теоретичната справка по-горе. От фиг.5а е очевидно, че проекцията на сумата от вектори е равна на сумата от проекциите на векторите. Ние изчисляваме тези прогнози:

Намираме крайната проекция на сумата от вектори:

Връзка на вектор с правоъгълна декартова координатна система в пространството

Запознаване с правоъгълна декартова координатна система в пространството се проведе в съответния урок, за предпочитане го отворете в нов прозорец.

В подредена система от координатни оси 0xyzос волНаречен ос х, ос 0 г – у-ос, и ос 0z – приложна ос.

с произволна точка Мвектор на космическата връзка

Наречен радиус векторточки Ми го проектираме върху всяка от координатните оси. Нека обозначим стойностите на съответните проекции:

Числа x, y, zНаречен координати на точка М, съответно абсцисата, ординатаИ апликация, и се записват като подредена точка от числа: M(x; y; z)(фиг. 6).

Нарича се вектор с единична дължина, чиято посока съвпада с посоката на оста единичен вектор(или ортом) брадви. Означаваме с

Съответно единичните вектори на координатните оси вол, Ой, Оз

Теорема.Всеки вектор може да се разложи на единичните вектори на координатните оси:

(2)

Равенство (2) се нарича разширение на вектора по координатните оси. Коефициентите на това разширение са проекциите на вектора върху координатните оси. По този начин коефициентите на разширение (2) на вектора по координатните оси са координатите на вектора.

След избор на определена координатна система в пространството, векторът и тройката от неговите координати се определят еднозначно взаимно, така че векторът може да се запише във формата

Векторните изображения във формата (2) и (3) са идентични.

Състоянието на колинеарни вектори в координати

Както вече отбелязахме, векторите се наричат ​​колинеарни, ако са свързани с релацията

Нека вектори . Тези вектори са колинеарни, ако координатите на векторите са свързани с релацията

,

тоест координатите на векторите са пропорционални.

Пример 6Дадени вектори . Колинеарни ли са тези вектори?

Решение. Нека разберем съотношението на координатите на тези вектори:

.

Координатите на векторите са пропорционални, следователно векторите са колинеарни или, което е същото, успоредни.

Дължина на вектор и косинуси на посоката

Поради взаимната перпендикулярност на координатните оси дължината на вектора

е равна на дължината на диагонала на правоъгълен паралелепипед, построен върху векторите

и се изразява с равенството

(4)

Векторът е напълно дефиниран чрез указване на две точки (начало и край), така че координатите на вектора могат да бъдат изразени чрез координатите на тези точки.

Нека началото на вектора в дадената координатна система е в точката

и краят е в точката

От равенството

Следва това

или в координатна форма

следователно координатите на вектора са равни на разликите на едноименните координати на края и началото на вектора . Формула (4) в този случай приема формата

Определя се посоката на вектора насочващи косинуси . Това са косинусите на ъглите, които векторът сключва с осите вол, ОйИ Оз. Нека обозначим съответно тези ъгли α , β И γ . Тогава косинусите на тези ъгли могат да бъдат намерени по формулите

Насочващите косинуси на вектора също са координатите на вектора на вектора и следователно вектора на вектора

.

Като се има предвид, че дължината на векторния вектор е равна на една единица, т.е.

,

получаваме следното равенство за насочващите косинуси:

Пример 7Намерете дължината на вектор х = (3; 0; 4).

Решение. Дължината на вектора е

Пример 8Дадени точки:

Разберете дали триъгълникът, построен върху тези точки, е равнобедрен.

Решение. Използвайки формулата за дължина на вектора (6), намираме дължините на страните и откриваме дали две от тях са еднакви:

Намерени са две равни страни, така че няма нужда да се търси дължината на третата страна, а дадения триъгълник е равнобедрен.

Пример 9Намерете дължината на вектор и косинусите на неговата посока, ако .

Решение. Координатите на вектора са дадени:

.

Дължината на вектора е равна на корен квадратен от сумата от квадратите на координатите на вектора:

.

Намиране на косинуси на посоката:

Решете сами задачата върху векторите и след това вижте решението

Операции с вектори, дадени в координатна форма

Нека са дадени два вектора и дадени чрез техните проекции:

Нека посочим действия върху тези вектори.

1. Допълнение:

или какво е същото

(когато се добавят два вектора, се добавят координатите със същото име).