ВЕКТОР. ҮЙЛ АЖИЛЛАГААДЭЭДВЕКТОР. СКАЛАР,
ВЕКТОР, ВЕКТОРЫН ХОЛИМОГ БҮТЭЭГДЭХҮҮН.
1. ВЕКТОР, ВЕКТОР ДЭЭРХ ҮЙЛ АЖИЛЛАГАА.
Үндсэн тодорхойлолтууд.
Тодорхойлолт 1.Сонгосон нэгжийн систем дэх тоон утгаараа бүрэн тодорхойлогддог хэмжигдэхүүнийг нэрлэдэг скалярэсвэл скаляр .
(Биеийн жин, эзэлхүүн, цаг хугацаа гэх мэт)
Тодорхойлолт 2.Тоон утга ба чиглэлээр тодорхойлогддог хэмжигдэхүүнийг нэрлэнэ вектор эсвэл вектор .
(Шилжилт, хүч, хурд гэх мэт)
Тэмдэглэл: , эсвэл , .
Геометрийн вектор нь чиглэсэн сегмент юм.
Векторын хувьд - цэг А- эхлэх цэг INнь векторын төгсгөл юм.
Тодорхойлолт 3.Модуль вектор нь AB сегментийн урт юм.
Тодорхойлолт 4.Модуль нь тэг байх векторыг нэрлэнэ тэг , заасан байна.
Тодорхойлолт 5.Зэрэгцээ шулуун эсвэл нэг шулуун дээр байрлах векторуудыг дуудна collinear . Хэрэв хоёр коллинеар вектор ижил чиглэлтэй бол тэдгээрийг дуудна хамтарсан чиглэлтэй .
Тодорхойлолт 6.Хоёр векторыг авч үзнэ тэнцүү , Хэрэв тэд хамтран найруулсан ба модулийн хувьд тэнцүү байна.
Вектор дээрх үйлдлүүд.
1) Вектор нэмэх.
Def. 6.нийлбэр хоёр вектор бөгөөд эдгээр векторууд дээр баригдсан параллелограммын диагональ нь тэдгээрийн хэрэглээний нийтлэг цэгээс ирдэг. (параллелограммын дүрэм).
Зураг 1.
Def. 7.Гурван векторын нийлбэр , , нь эдгээр векторууд дээр баригдсан параллелепипедийн диагональ юм (параллелепипедийн дүрэм).
Def. 8.Хэрэв А, IN, ХАМТ дурын цэгүүд бол + = (гурвалжингийн дүрэм).
2-р зураг
Нэмэлт шинж чанарууд.
1 О . + = + (нүүлгэн шилжүүлэх хууль).
2 О . + ( + ) = ( + ) + = ( + ) + (ассоциатив хууль).
3 О . + (– ) + .
2) Векторуудыг хасах.
Def. 9.Доод ялгаа вектор ба векторыг ойлгох = - ийм + = .
Параллелограмм дээр энэ нь өөр юм диагональ SD (1-р зургийг үз).
3) Векторыг тоогоор үржүүлэх.
Def. 10. ажил вектороос скаляр к вектор гэж нэрлэдэг
= к = к ,
урт ка , болон чиглэл нь:
1. векторын чиглэлтэй давхцдаг if к > 0;
2. векторын чиглэлийн эсрэг байвал к < 0;
3. дур мэдэн хэрэв к = 0.
Векторыг тоогоор үржүүлэх шинж чанарууд.
1 О . (к + л ) = к + л .
к ( + ) = к + к .
2 о . к (л ) = (kl ) .
3 о . 1 = , (–1) = – , 0 = .
Вектор шинж чанарууд.
Def. арван нэгэн.Хоёр вектор ба гэж нэрлэдэг collinear хэрэв тэдгээр нь дээр байрладаг бол зэрэгцээ шугамуудэсвэл цагт нэг шулуун шугам.
Тэг вектор нь ямар ч вектортой коллинеар байна.
Теорем 1.Хоёр тэгээс өөр вектор ба шугаман, тэдгээр нь пропорциональ байх үед өөрөөр хэлбэл.
= к , к - скаляр.
Def. 12.Гурван векторыг , , гэж нэрлэдэг хавтгай хэрэв тэдгээр нь ямар нэг хавтгайтай параллель эсвэл дотор нь хэвтэж байвал.
Теорем 2.Тэг биш гурван вектор, , хавтгай, тэдгээрийн аль нэг нь нөгөө хоёрын шугаман хослол байх үед, өөрөөр хэлбэл.
= к + л , к , л - скаляр.
Векторын тэнхлэг дээрх проекц.
Теорем 3.Векторын тэнхлэг дээрх проекц (чиглүүлсэн шугам) лвекторын урт ба векторын чиглэл ба тэнхлэгийн чиглэлийн хоорондох өнцгийн косинусын үржвэртэй тэнцүү байна, i.e. = а в os , = ( , л).
2. ВЕКТОРЫН КООРДИНАТ
Def. 13.Координатын тэнхлэг дээрх вектор проекц Өө, OU, Оздуудсан вектор координат. Тэмдэглэл: а x , а y , а z .
Вектор урт: 
Жишээ:Векторын уртыг тооцоол.
Шийдэл:
Цэгүүдийн хоорондох зай 
Тэгээд 
томъёогоор тооцоолно: .
Жишээ: M (2,3,-1) ба K (4,5,2) цэгүүдийн хоорондох зайг ол.
Координат хэлбэрийн векторууд дээрх үйлдлүүд.
Өгөгдсөн векторууд = а x , а y , а z ба = б x , б y , б z .
1. ( )= а x б x , а y б y , а z б z .
2. = а x , а y , а z, хаана - скаляр.
Векторуудын скаляр үржвэр.
Тодорхойлолт:Хоёр векторын скаляр үржвэрийн дор ба
Эдгээр векторуудын урт ба тэдгээрийн хоорондох өнцгийн косинусын үржвэртэй тэнцүү тоо гэж ойлгогддог, өөрөөр хэлбэл. = , - векторуудын хоорондох өнцөг ба .
Цэг бүтээгдэхүүний шинж чанар:
1. =
2. ( + ) =
3.
4.
5. , скаляр хаана байна.
6. хоёр вектор перпендикуляр (ортогональ) бол .
7. хэрвээ зөвхөн хэрэв 
.
Координат хэлбэрийн скаляр бүтээгдэхүүн нь дараах хэлбэртэй байна. 
,
хаана ба .
Жишээ:ба векторуудын скаляр үржвэрийг ол
Шийдэл:
Вектор барих векторууд.
Тодорхойлолт: Хоёр векторын вектор үржвэр бөгөөд үүнийг вектор гэж ойлгодог.
Модуль нь эдгээр векторууд дээр баригдсан параллелограммын талбайтай тэнцүү байна, жишээлбэл. 
, ба векторуудын хоорондох өнцөг хаана байна
Энэ вектор нь үржүүлсэн векторуудад перпендикуляр, өөрөөр хэлбэл.
Хэрэв векторууд нь коллинеар биш бол векторуудын зөв гурвалсан хэсгийг бүрдүүлнэ.
Бүтээгдэхүүн хоорондын шинж чанар:
1. Хүчин зүйлсийн дарааллыг өөрчлөх үед вектор бүтээгдэхүүн нь модулийг хадгалан, тэмдгээ эсрэгээр өөрчилдөг, i.e. 
2 .Вектор квадрат нь тэг вектортой тэнцүү, өөрөөр хэлбэл.
3
.Скаляр коэффициентийг вектор үржвэрийн тэмдгээс гаргаж авч болно, өөрөөр хэлбэл. 
4
.Дурын гурван векторын хувьд тэгш байдал 
5 .Хоёр векторын коллинеар байх шаардлагатай ба хангалттай нөхцөл ба :
Координат хэлбэрийн вектор бүтээгдэхүүн.
Хэрэв векторуудын координат ба , Дараа нь тэдгээрийн вектор үржвэрийг дараах томъёогоор олно.
.
Дараа нь хөндлөн үржвэрийн тодорхойлолтоос үзэхэд параллелограммын талбайг векторууд дээр барьж, дараах томъёогоор тооцоолно.
Жишээ:Орой (1;-1;2), (5;-6;2), (1;3;-1) бүхий гурвалжны талбайг тооцоол.
Шийдэл: 
.
Дараа нь ABC гурвалжны талбайг дараах байдлаар тооцоолно.
,
Векторуудын холимог бүтээгдэхүүн.
Тодорхойлолт:Векторуудын холимог (вектор-скаляр) үржвэр нь дараахь томъёогоор тодорхойлогддог тоо юм. 
.
Холимог бүтээгдэхүүний шинж чанар:
1.
Холимог бүтээгдэхүүн нь түүний хүчин зүйлсийн мөчлөгийн өөрчлөлтөөр өөрчлөгддөггүй, өөрөөр хэлбэл. 
.
2. Хоёр хөрш зэргэлдээ хүчин зүйл солигдох үед холимог бүтээгдэхүүн нь тэмдэгээ эсрэгээр нь өөрчилдөг, өөрөөр хэлбэл. .
3 .Гурван вектор копланар байх зайлшгүй ба хангалттай нөхцөл : =0.
4 .Гурван векторын холимог үржвэр нь эдгээр векторууд дээр баригдсан параллелепипедийн эзэлхүүнтэй тэнцүү бөгөөд хэрэв эдгээр векторууд баруун гурвалсан бол нэмэх тэмдгээр, зүүн гурвалсан бол хасах тэмдгээр авсан, өөрөөр хэлбэл. .
Хэрэв мэддэг бол координатуудвекторууд ,
Дараа нь холимог бүтээгдэхүүнийг дараах томъёогоор олно. 
Жишээ:Векторуудын холимог үржвэрийг тооцоол.
Шийдэл: 
3. Векторын системийн үндэс.
Тодорхойлолт.Векторын системийг нэг орон зайд хамаарах хэд хэдэн вектор гэж ойлгодог Р.
Сэтгэгдэл.Хэрэв систем нь хязгаарлагдмал тооны векторуудаас бүрддэг бол тэдгээрийг өөр өөр индекстэй ижил үсгээр тэмдэглэнэ.
Жишээ. 
Тодорхойлолт. = хэлбэрийн дурын вектор 
векторуудын шугаман хослол гэж нэрлэдэг. Тоонууд нь шугаман хослолын коэффициентууд юм.
Жишээ. 
.
Тодорхойлолт. Хэрэв вектор нь векторуудын шугаман хослол бол , тэгвэл бид векторыг векторуудын хувьд шугаман байдлаар илэрхийлнэ гэж хэлдэг .
Тодорхойлолт.Векторуудын систем гэж нэрлэдэг шугаман бие даасан, хэрэв системийн векторуудын аль нь ч бусад векторуудын шугаман хослол байж чадахгүй бол. Үгүй бол системийг шугаман хамааралтай гэж нэрлэдэг.
Жишээ. Вектор систем 
вектороос хойш шугаман хамааралтай 
.
Үндсэн тодорхойлолт.Векторын систем нь дараахь тохиолдолд үндэс болно.
1) шугаман бие даасан,
2) түүгээр дамжин өнгөрөх орон зайн дурын вектор шугаман хэлбэрээр илэрхийлэгдэнэ.
Жишээ 1Сансрын суурь: .
2.
Векторуудын системд 
векторууд нь суурь болно: , учир нь 
вектороор шугаман хэлбэрээр илэрхийлэгдэнэ.
Сэтгэгдэл.Өгөгдсөн векторын системийн үндсийг олохын тулд та дараахь зүйлийг хийх хэрэгтэй.
1) матриц дахь векторуудын координатыг бичих,
2) энгийн хувиргалтыг ашиглан матрицыг гурвалжин хэлбэрт оруулах,
3) матрицын тэг биш мөрүүд нь системийн үндэс болно,
4) суурь дахь векторын тоо нь матрицын зэрэгтэй тэнцүү байна.
1. Нэмэлт. a ба b хоёр вектор байг. Дурын O цэгээс бид OA = a векторыг, үр дүнд нь А цэгээс - AB = b векторыг салгана. OB векторыг нийлбэр гэж нэрлэдэга+ бa ба b векторууд (Зураг 6), векторуудын нийлбэрийг олох үйлдэл нь тэдгээрийн нэмэгдэл юм.
Векторуудын нэмэлтийг зөв тодорхойлсон эсэхийг шалгацгаая, өөрөөр хэлбэл. векторуудын нийлбэр нь О цэгийн сонголтоос хамаарахгүй.Үүний тулд өөр Q цэгийг авч QC = a ба CD = b векторуудыг хойш тавь. QC = OA = a тул хоёр векторын тэгш байдлын шалгуураар (1.8) бид OQ = AC гэдгийг олж авна. Үүний нэгэн адил AB = CD = b тэгшитгэлээс АС = BD гэж гарна. Үүний үр дүнд OQ = BD, мөн (1.8) шалгуурыг дахин хэрэглэснээр бид нотлох ёстой OB = QD-г олж авна (Зураг 7).
Гурвалжингийн дүрэм нь хоёр векторын нийлбэрийн тодорхойлолтоос шууд гардаг.
(2.1) О, А ба В дурын гурван цэгийн хувьд OA + AB = OB.
Түүнчлэн, сургуулийн геометрийн хичээлээс мэдэгдэж байгаачлан О, А, В гэсэн гурван цэгийн хувьд OB сегментийн урт нь OA ба AB хэрчмүүдийн уртын нийлбэрээс хэтрэхгүй бөгөөд |OB| = |OA| + |AB| А цэг нь [OB] сегмент дээр байрлах үед л хүрнэ. Энэ тэгш бус байдлыг ихэвчлэн гурвалжингийн тэгш бус байдал гэж нэрлэдэг. Векторуудын нийлбэрийн тодорхойлолт нь үүнийг вектор хэлбэрээр бичих боломжийг танд олгоно.
(2.2) |а + b| |а| + |b| .
(2.2)-д заасан тэгш байдал нь зөвхөн а ба b векторууд нэг чиглэлд, бусад тохиолдолд тэгш бус байдал нь хатуу байх тохиолдолд л хүрнэ. |a+b| тэгшитгэлийг бич = |a|+|b| дурын векторуудын хувьд - бүдүүлэг алдаа.
2. Вектор нэмэх үндсэн шинж чанарууд. Үүнд:
(C1) дурын гурван векторын хувьд a, b ба c (a+b)+c = a+(b+c) (ассоциатив).
(С2) Дурын хоёр векторын хувьд a ба b a+b = b+a (коммутатив).
(С3) Аливаа векторын хувьд a a+0 = a.
(С4) А ба В дурын хоёр цэгийн хувьд AB + BA = 0.
IN
Эд хөрөнгийг (С1) баталцгаая. Үүнийг хийхийн тулд бид OA = a, AB = b, BC = c векторуудыг дараалан хойшлуулна. Вектор нэмэхийн тодорхойлолтоор (a + b) + c = OB + BC, a + (b + c) = OA + AC. Гэхдээ OB + BC \u003d OA + AC \u003d OS (Зураг 9).
8-р зурагт байгааг анхаарна ууОК = AB. Тиймээс шударга байна
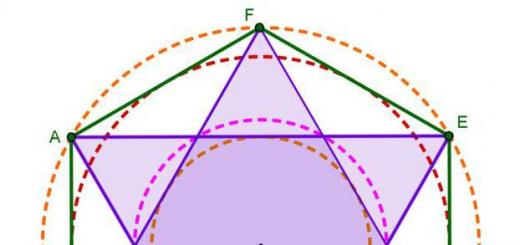
(2.3) Параллелограммын дүрэм: Коллинеар бус a ба b векторуудын нийлбэр нь векторууд дээр баригдсан OABS параллелограммын диагональ OB-тай тэнцүү байна. 2 OA = a ба OS = b.
Нэмж дурдахад, дээрх холбоодын нотолгооноос бид олж авдаг
(2.4) Олон өнцөгтийн дүрэм. Тодорхой дарааллаар авсан хэд хэдэн векторыг нэмэхийн тулд тэдгээрийг нэг нэгээр нь хойш нь тавьж, вектор бүрийн төгсгөл нь дараагийнх нь эхлэл болж, эхнийх нь төгсгөлд нь залгах ёстой.
Бид энэ дүрмийг зөвхөн гурван векторын хувьд нотолсон боловч дээрх үндэслэлийг ямар ч тооны нэр томъёонд хялбархан сунгаж болно.
П
(2.5) Хаалттай хэлхээний дүрэм. Хэд хэдэн векторын нийлбэр нь тэгтэй тэнцүү бөгөөд зөвхөн дараалан хойшлуулах үед тэдгээр нь хаалттай гинж үүсгэдэг, өөрөөр хэлбэл. сүүлчийнх нь төгсгөл нь эхнийхтэй давхцдаг.
(2.6) Дасгал хийх. Параллелепипедийн дүрмийг батална уу: нэг хавтгайд параллель биш гурван векторыг нэмэхийн тулд тэдгээрийг нэг О цэгээс хойш тавьж, үүссэн гурван сегментийг параллелепипед болгон дуусгаж, О цэгээс энэ параллелепипедийн диагональ зурах хэрэгтэй. энэ нь хүссэн нийлбэр байх болно (Зураг 10).
Вектор нэмэхийн ассоциатив байдал нь тодорхой дарааллаар авсан гурван векторын нийлбэр нь эхлээд эхний хоёр векторыг нэмж, дараа нь гурав дахь векторыг нэмэх, эсвэл эхлээд хоёр, гурав дахь векторын нийлбэрийг олох эсэхээс хамаарахгүй болохыг харуулж байна. векторууд, дараа нь эхний . Энэ нь бид гурван векторын нийлбэрийг хаалтанд хэрхэн байрлуулах талаар бодохгүйгээр a + b + c гэж бичиж болно гэсэн үг юм. Алгебрийн хичээлийн явцад хэрэв энэ шинж чанар нь гурван гишүүний хувьд биелэх юм бол дурын тооны хувьд ч биелнэ, өөрөөр хэлбэл бид дурын вектор нийлбэр a + b + c + ... + -ийг санаа зовохгүйгээр бичиж болно гэдгийг харуулах болно. хаалтуудыг байрлуулах арга замын тухай d. Мөн хувирах шинж чанар (C2) нь бид энэ нийлбэрийг өөрчлөхгүйгээр доторх нэр томъёог дур зоргоороо өөрчлөх боломжтой гэдгийг харуулж байна. Энэ бол ассоциаци болон хувирах байдлын утга юм.
3
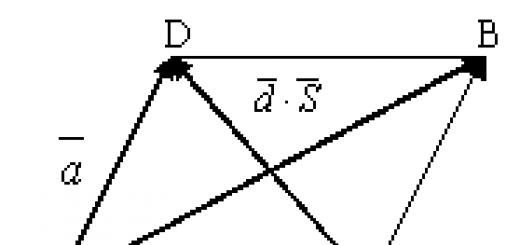
Дурын О цэгээс OA=a ба OB=b векторуудыг салгая. Мэдээжийн хэрэг, OB-тай хамт OA өгдөг цорын ганц вектор бол BA вектор юм. Тиймээс,
(2.7) дурын хоёр вектор нь зөвхөн нэг л ялгаатай байна. Үүнийг бүтээхийн тулд та векторуудыг нэг цэгээс хойшлуулж, хоёр дахь төгсгөлийг эхний төгсгөлтэй холбох хэрэгтэй (Зураг 11).
З
a–b = a+(–b).
Өөрөөр хэлбэл, нэг векторыг нөгөө вектороос хасах нь эхний векторыг хоёр дахь векторын эсрэг вектор дээр нэмэхтэй адил юм.
a ба b векторууд коллинеар биш байг. Дараа нь O, A, B цэгүүд гурвалжин үүсгэнэ. Хэрэв бид үүнийг OASV параллелограмм болгон гүйцээж өгвөл түүний диагональ болно 
a + b нийлбэр ба диагональыг илэрхийлнэ 
- ялгаа a-b (Зураг 12). Энэ нь параллелограммын дүрэмд хэрэгтэй нэмэлт юм.
Тэгш байдлыг (2.8) цэвэр алгебрийн аргаар баталж болно. Үнэхээр x = a+(–b) бол x+b = a+(–b)+b = a+0 = а. Мөн a–b ялгаа нь өөр утгагүй болохыг алгебрийн аргаар харуулж болно: x+b = а (x+b)+(–b) = a+(–b) x+(b+(–b)) = a+(–b) x+0=a+(–b) x = a+(–b). Эдгээр бүх өөрчлөлтүүд нь зөвхөн нэмэлт (C1)-(C4) (шалга!)-ын үндсэн шинж чанарт тулгуурладгийг харуулахын тулд бид зориудаар бүх өөрчлөлтүүдийг нарийвчлан бичсэн. Таны алгебрийн хичээлээр судлах вектор орон зайн ерөнхий онолд эдгээр шинж чанаруудыг вектор нэмэх аксиомууд болгон авдаг бөгөөд нэмэхийн бусад бүх шинж чанаруудыг тэдгээрээс гаргаж авдаг.
4. Векторыг тоогоор үржүүлэх. Векторыг тоогоор үржүүлэх нь векторын үржвэрийг тоогоор олох үйлдэл юм. Тэг биш a вектор ба х тооны үржвэр нь "xa" гэж тэмдэглэгдсэн вектор бөгөөд дараах хоёр нөхцлийг хангана.
(P1) | га | = |x||a| ; (P2) га мөн хэрэв x 0, мөн га мөн хэрэв x<0.
Тэг векторын аль ч тооны үржвэр нь тодорхойлолтоор 0-тэй тэнцүү байна.
Нөхцөл (A1) хүчинтэй хэвээр байнаx= 0, гэхдээ энэ тохиолдолд нөхцөл (A2) нь x дээр зөрчигдөж байна<0 (из-за чего случай нулевого вектора и приходится рассматривать отдельно). Однако, при любых а и х векторы а и ха коллинеарны (почему?).
xa = 0 гэдгийг анхаарна уу |га| = 0 |x||a| = 0 |x| = 0 эсвэл |a| = 0 X = 0 эсвэл a = 0. Тэгэхээр,
(2.9) Вектор ба тооны үржвэр нь зөвхөн тоо эсвэл вектор нь тэгтэй тэнцүү байх тохиолдолд л тэгтэй тэнцүү байна.
Тэг биш x тоо ба а векторыг өгье. Дурын O цэгээс бид OA = a векторыг хойш тавьж, вектор байгуулахыг оролдоноҮХЭР= га. a ба xa векторууд нь коллинеар байх ёстой тул сегмент 
шулуун (OA) дээр байх ёстой бөгөөд (A1) нөхцлийн дагуу урт нь |x||a|-тай тэнцүү байх ёстой. Яг хоёр ийм сегмент байдаг бөгөөд тэдгээрийн нэг нь (үүнийг нэрлэе 
) хамтран найруулж байна 
, нөгөө нь (үүнийг нэрлэе 
) эсрэг чиглэлтэй байна 
(Зураг 13). (P2) нөхцөл рүү буцаж ирэхэд бид үүнийг харж байна 
=
x > 0-ийн хувьд ба 
=
x дээр< 0.
Т
Векторуудыг тоогоор үржүүлэх үндсэн шинж чанарууд нь дараахь зүйлийг агуулна.
(Y1) Аливаа векторын хувьд a 1a=a (өөрөөр хэлбэл 1-ээр үржүүлэхэд вектор өөрчлөгдөхгүй).
(Y2) Дурын тооны x, y ба векторын хувьд x(ya) = (xy)a (ассоциатив).
(Y3) Дурын х, у болон векторын хувьд a (x + y) a = xa + ya (тоо нэмэхтэй холбоотой үржүүлгийн тархалт).
(Y4) Дурын х тоо ба a, b векторуудын хувьд x(a + b) = xa + xb (вектор нэмэхтэй холбоотойгоор үржүүлгийн тархалт).
Эдгээр шинж чанаруудын эхнийх нь тодорхойлолтоос шууд гардаг (шалга!). Үлдсэн нотолгоог L.S.-ийн 14-16-р хуудаснаас олж болно. Атанасян ба В.Т. Базылев "Геометр" (1-р хэсэг).
Векторыг тоогоор үржүүлэх дараах шинж чанаруудыг бид мөн тэмдэглэж байна.
(2.10) Хэрэв а вектор тэгээс ялгаатай бол a/|a| нь вектор а-тай кодиректорын нэгж вектор юм. 3
Үнэн хэрэгтээ a ба a/|a| векторууд кодиректортой (учир нь 1/|a| > 0) ба |a/|a|| = |a|/|a| = 1.
(2.11) (–1)а = –а.
Үнэн хэрэгтээ векторыг тоогоор үржүүлэх тодорхойлолтоор (–1)а ба а векторууд эсрэгээрээ чиглэсэн бөгөөд тэдгээрийн урт нь тэнцүү байна.
5. Хамтарсан байдлын шинж тэмдэг.
(2.12) Вектор нь тэгээс өөр вектортой коллинеар байх шалгуур. Зөвхөн ийм тоо байгаа тохиолдолд b вектор нь тэг биш a вектортой коллинеар байнат, тэр b =тА. Түүнчлэн хэрэв a ба b векторууд кодиректортой бол t = |b| / |а|, хэрэв тэдгээр нь эсрэгээр чиглэсэн байвал т = – |б| / |а|.
a ба ta векторууд үргэлж нэгдмэл байдаг гэдгийг бид аль хэдийн тэмдэглэсэн. Үүний эсрэгээр, тэгээс өөр вектор а, коллинеар в векторыг авна. Хэрэв тэдгээр нь хоёр чиглэлтэй бол бид t = |b|/|a|-г тавина. Дараа нь |та| = |t||а| = (|b|/|a|)|a| = |b|, мөн ta вектор нь a-тай, тиймээс b-тэй координат байна. Тиймээс та = b шинж чанарын дагуу 1.7. Хэрвээ b, бид t = –|b|/|a|-г тогтоов. Мөн дахин |та| = |t||а| = (|b|/|a|)|a| = |b|, харин a векторын эсрэг чиглэсэн ta ба b векторууд (Н5) -ын дагуу кодиректортой байна. Тиймээс, энэ тохиолдолд, ta = б.
a вектор нь тэг биш гэсэн анхааруулга нь заримдаа тохиромжгүй байдаг. Дараа нь та үүнийг ашиглаж болно
(2.13) Хоёр векторын коллинеарийн тэмдэг. Хоёр вектор нь зөвхөн нэгийг нь нөгөөгөөр нь тоогоор үржүүлэх замаар илэрхийлэх боломжтой тохиолдолд л коллинеар болно.
Өгөгдсөн хоёр векторын ядаж нэг нь тэгтэй тэнцүү биш тохиолдолд энэ нь дээр батлагдсан. Хэрэв хоёр вектор хоёулаа тэг байвал нэгдүгээрт, тэдгээр нь хоорондоо уялдаатай, хоёрдугаарт, тэдгээрийн аль нэгийг нь дурын тоогоор үржүүлэх замаар нөгөөгөөсөө гаргаж авах боломжтой тул энэ тохиолдолд бүх зүйл эмх цэгцтэй байна.
6. Вектор дээрх үйлдлүүдэд параллелизмыг хадгалах.
(2.14) Параллелизмын тухай лемма. Хэрэв хоёр вектор зарим шулуун (хавтгай) -тай параллель байвал ижил шулуун (хавтгай) нь тэдгээрийн нийлбэртэй параллель байна. Хэрэв вектор нь шулуун (хавтгай) -тай параллель байвал ижил шулуун (хавтгай) нь түүний үржвэртэй ямар ч тоогоор параллель байна.
a ба b векторууд нь өгөгдсөн шулуунтай (хавтгай) параллель байя. Түүний дурын О цэгээс OA = a ба AB = b векторуудыг салгая. Дараа нь А ба В цэгүүд мөн энэ шулуун (хавтгай) дээр хэвтэнэ. Энэ нь a + b нийлбэрийг илэрхийлэх OB сегмент мөн тэнд хэвтэж байх бөгөөд энэ нь энэ шулуун шугамтай (хавтгай) параллель байна гэсэн үг юм.
Одоо дурын х тоог авч, ижил О цэгээс OS = xa векторыг хойш тавья. Хэрэв a \u003d 0 бол xa \u003d 0, тэг вектор нь ямар ч шулуун ба хавтгайтай параллель байна. Хэрэв тийм биш бол xa векторыг төлөөлж буй OS сегмент нь бүхэлдээ OA шулуун шугам дээр, тиймээс өгөгдсөн шулуун шугам (хавтгай) дээр байх болно. Иймд xa вектор нь энэ шулуунтай (хавтгай) параллель байх болно.
Векторууд. Вектортой үйлдэл. Энэ өгүүллээр бид вектор гэж юу болох, түүний уртыг хэрхэн олох, векторыг тоогоор хэрхэн үржүүлэх, мөн хоёр векторын нийлбэр, ялгавар, цэгийн үржвэрийг хэрхэн олох талаар ярилцах болно.
Ердийнх шиг, хамгийн шаардлагатай онолын зарим нь.
Вектор нь чиглэсэн сегмент, өөрөөр хэлбэл эхлэл ба төгсгөлтэй сегмент юм.
Энд А цэг нь векторын эхлэл, В цэг нь түүний төгсгөл юм.
Вектор нь урт ба чиглэл гэсэн хоёр параметртэй.
Векторын урт нь векторын эхлэл ба төгсгөлийг холбосон сегментийн урт юм. Векторын уртыг тэмдэглэв
Хоёр векторыг тэнцүү гэж нэрлэдэгхэрэв тэдгээр нь ижил урттай бөгөөд зэрэгцсэн байвал.
Хоёр векторыг нэрлэдэг хамтарсан чиглэлтэй, хэрэв тэдгээр нь параллель шулуунууд дээр хэвтэж, нэг чиглэлд чиглүүлсэн бол: векторууд ба хамтран чиглэсэн:
Хоёр векторыг параллель шулуун дээр хэвтэж, эсрэг чиглэлд чиглүүлсэн бол эсрэг чиглэлтэй гэж нэрлэдэг: векторууд ба , түүнчлэн эсрэг чиглэлд чиглэгддэг.
Зэрэгцээ шулуун дээр байрлах векторуудыг коллинеар гэж нэрлэдэг: векторууд , ба коллинеар байдаг.
Вектор бүтээгдэхүүнхэрэв title="k>0) бол уг тоог вектор руу чиглэсэн вектор гэж нэрлэдэг">, и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :!}
руу хоёр вектор нэмнэба , та векторын эхлэлийг векторын төгсгөлтэй холбох хэрэгтэй. Нийлбэр вектор нь векторын эхлэлийг векторын төгсгөлтэй холбодог.
Энэ вектор нэмэх дүрмийг гэж нэрлэдэг гурвалжингийн дүрэм.
Хоёр вектор нэмэх параллелограммын дүрэм, та векторыг нэг цэгээс хойшлуулж, параллелограмм болгон дуусгах хэрэгтэй. Нийлбэр вектор нь векторуудын гарал үүслийг параллелограммын эсрэг булантай холбодог.
Хоёр векторын ялгаанийлбэрээр тодорхойлогддог: векторуудын ялгавар ба ийм вектор бөгөөд векторын нийлбэрээр векторыг өгөх болно:
Тиймээс дараах хоёр векторын ялгааг олох дүрэм: вектороос векторыг хасахын тулд эдгээр векторуудыг нэг цэгээс хойшлуулах хэрэгтэй. Ялгаа вектор нь векторын төгсгөлийг векторын төгсгөлд холбодог (өөрөөр хэлбэл хасахын төгсгөлийг хасах төгсгөлд):
Олох вектор ба вектор хоорондын өнцөг, та эдгээр векторуудыг нэг цэгээс хойшлуулах хэрэгтэй. Векторууд байрлах туяанаас үүссэн өнцгийг векторуудын хоорондох өнцөг гэнэ.
Хоёр векторын скаляр үржвэр нь эдгээр векторуудын урт ба тэдгээрийн хоорондох өнцгийн косинусын үржвэртэй тэнцүү тоо юм.
Би танд Open Task Bank-аас асуудлыг шийдэхийг санал болгож байна , дараа нь ВИДЕО СУРГАЛТЫН тусламжтайгаар шийдлээ шалгана уу:
1 . Даалгавар 4 (No 27709)
Тэгш өнцөгтийн хоёр тал A B C D 6 ба 8-тай тэнцүү ба векторуудын ялгааны уртыг ол.
2. Даалгавар 4 (No 27710)
Тэгш өнцөгтийн хоёр тал A B C D 6 ба 8. ба векторуудын скаляр үржвэрийг ол. (өмнөх даалгавраас зураг зурах).
3 . Даалгавар 4 (No 27711)
Тэгш өнцөгтийн хоёр тал A B C D О. ба векторуудын нийлбэрийн уртыг ол.
4 . Даалгавар 4 (No 27712)
Тэгш өнцөгтийн хоёр тал A B C D 6 ба 8. Диагональууд нь цэг дээр огтлолцдог О. ба векторуудын ялгааны уртыг ол. (өмнөх даалгавраас зураг зурах).
5 . Даалгавар 4 (No 27713)
Ромбын диагональ A B C D 12 ба 16. Векторын уртыг ол.
6. Даалгавар 4 (No 27714)
Ромбын диагональ A B C D 12 ба 16. + векторын уртыг ол.
7. Даалгавар 4 (No 27715)
Ромбын диагональ A B C Dнь 12 ба 16. векторын уртыг ол - .(өмнөх бодлогоос зурсан).
8. Даалгавар 4 (No 27716)
Ромбын диагональ A B C D 12 ба 16. - векторын уртыг ол.
9 . Даалгавар 4 (No 27717)
Ромбын диагональ A B C Dцэг дээр огтлолцоно Оба 12 ба 16-тай тэнцүү. + векторын уртыг ол.
10 . Даалгавар 4 (No 27718)
Ромбын диагональ A B C Dцэг дээр огтлолцоно Оба 12 ба 16-тай тэнцүү байна. векторын уртыг ол - .(өмнөх даалгавраас зурах).
11. Даалгавар 4 (No 27719)
Ромбын диагональ A B C Dцэг дээр огтлолцоно Оба 12 ба 16-тай тэнцүү ба векторуудын скаляр үржвэрийг ол (өмнөх бодлогоос зурсан).
12 . Даалгавар 4 (No 27720)
ABCтэнцүү + векторын уртыг ол.
13 . Даалгавар 4 (No 27721)
Тэгш талт гурвалжны талууд ABCтэнцүү 3. - векторын уртыг ол.(өмнөх даалгаврын зураг).
14 . Даалгавар 4 (No 27722)
Тэгш талт гурвалжны талууд ABC 3-тай тэнцүү ба векторуудын скаляр үржвэрийг ол. (өмнөх даалгавраас зураг зурах).
Магадгүй таны хөтөч дэмжигдээгүй байна. "Улсын нэгдсэн шалгалтын цаг" симуляторыг ашиглахын тулд татаж аваад үзээрэй
Firefox
Тодорхойлолт Бодит тооны эрэмбэлэгдсэн цуглуулгыг (x 1 , x 2 , ... , x n) n гэнэ. n хэмжээст вектор, мөн тоонууд x i (i = 1,...,n) - бүрэлдэхүүн хэсгүүдэсвэл координат,
Жишээ. Жишээлбэл, нэг автомашины үйлдвэр нь нэг ээлжинд 50 автомашин, 100 ачааны машин, 10 автобус, автомашины 50 иж бүрдэл, ачааны машин, автобусны 150 иж бүрдэл үйлдвэрлэх ёстой бол энэ үйлдвэрийн үйлдвэрлэлийн хөтөлбөрийг дараах байдлаар бичиж болно. вектор (50, 100, 10, 50, 150), таван бүрэлдэхүүн хэсэгтэй.
Тэмдэглэгээ. Векторуудыг тод жижиг үсгээр эсвэл дээд талд нь баар эсвэл сумтай үсгээр тэмдэглэнэ, жишээлбэл, аэсвэл. Хоёр векторыг нэрлэдэг тэнцүүхэрэв тэдгээр нь ижил тооны бүрэлдэхүүн хэсгүүдтэй бөгөөд тэдгээрийн харгалзах бүрэлдэхүүн хэсгүүд нь тэнцүү бол.
Вектор бүрэлдэхүүн хэсгүүдийг сольж болохгүй, жишээлбэл (3, 2, 5, 0, 1)ба (2, 3, 5, 0, 1) өөр векторууд.
Вектор дээрх үйлдлүүд.ажил
x= (x 1 , x 2 , ... ,x n) бодит тооλ вектор гэж нэрлэдэгλ x= (λ x 1 , λ x 2 , ... , λ x n).
нийлбэрx= (x 1 , x 2 , ... ,x n) ба y= (y 1 , y 2 , ... ,y n) -ийг вектор гэнэ x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).
Векторуудын орон зай.Н -хэмжээст вектор орон зай Р n нь бодит тоогоор үржүүлэх болон нэмэх үйлдлүүдийг тодорхойлсон бүх n хэмжээст векторуудын олонлогоор тодорхойлогддог.
Эдийн засгийн дүрслэл. n хэмжээст вектор орон зайн эдийн засгийн дүрслэл: барааны орон зай (бараа). Доод барааБид тодорхой газар тодорхой цагт худалдаанд гарсан зарим бараа, үйлчилгээг ойлгох болно. Хязгаарлагдмал тооны бараа байгаа гэж үзье n; Хэрэглэгчийн худалдаж авсан тэдгээрийн тоо хэмжээг багц барааны хэлбэрээр тодорхойлдог
x= (x 1 , x 2 , ..., x n),
Энд x i нь хэрэглэгчийн худалдан авсан i-р барааны хэмжээг илэрхийлнэ. Бид бүх барааг дур зоргоороо хуваах шинж чанартай гэж үзэх бөгөөд ингэснээр тэдгээрийн сөрөг бус тоо хэмжээг худалдан авч болно. Дараа нь бүх боломжит барааны багц нь барааны орон зайн векторууд юм C = ( x= (x 1 , x 2 , ... , x n) x i ≥ 0, i =).
Шугаман бие даасан байдал.
Систем д 1 , д 2 , ... , д m n хэмжээст векторууд гэж нэрлэдэг шугаман хамааралтайийм тоо байгаа болλ 1 , λ 2 , ... , λ м , үүнээс дор хаяж нэг нь тэгээс ялгаатай нь тэгш байдлыг ханганаλ1 д 1 + λ2 д 2+...+λм дм = 0; өөрөөр хэлбэл энэ векторын системийг гэж нэрлэдэг шугаман бие даасан, өөрөөр хэлбэл, энэ тэгш байдал нь зөвхөн бүх тохиолдолд л боломжтой юм 
. Векторуудын шугаман хамаарлын геометрийн утга Р 3 , чиглэгдсэн сегмент гэж тайлбарлавал дараах теоремуудыг тайлбарла.
Теорем 1. Нэг вектороос бүрдэх систем нь зөвхөн энэ вектор тэг байх тохиолдолд шугаман хамааралтай болно.
Теорем 2. Хоёр вектор шугаман хамааралтай байхын тулд тэдгээр нь коллинеар (параллель) байх нь зайлшгүй бөгөөд хангалттай юм.
Теорем 3 . Гурван вектор шугаман хамааралтай байхын тулд тэдгээр нь хоорондоо уялдаатай (нэг хавтгайд хэвтэж) байх шаардлагатай бөгөөд хангалттай.
Зүүн ба баруун гурвалсан векторууд. Хавсарсан бус векторуудын гурвалсан тоо a, b, cдуудсан зөв, хэрэв тэдгээрийн нийтлэг гарал үүслийн ажиглагч векторуудын төгсгөлийг тойрч байвал a, b, cэнэ дарааллаар цагийн зүүний дагуу явж байх шиг байна. Үгүй бол a, b, c -зүүн гурав дахин. Бүх баруун (эсвэл зүүн) гурвалсан векторууд гэж нэрлэгддэг тэнцүү чиглэсэн.
Суурь ба координат. Тройка д 1, д 2 , д 3 давхцаагүй векторууд Р 3 дуудсан суурь, мөн векторууд өөрсдөө д 1, д 2 , д 3 - үндсэн. Аливаа вектор асуурь векторуудын хувьд өвөрмөц байдлаар өргөжүүлж болно, өөрөөр хэлбэл хэлбэрээр төлөөлүүлж болно
А= x 1 д 1 + x2 д 2 + x 3 д 3, (1.1)
(1.1) өргөтгөлийн x 1 , x 2 , x 3 тоонуудыг дуудна координатуудаүндсэн дээр д 1, д 2 , д 3 ба тэмдэглэгдсэн байна а(x 1 , x 2 , x 3).
Ортонормаль суурь. Хэрэв векторууд д 1, д 2 , д 3 нь хос перпендикуляр бөгөөд тус бүрийн урт нь нэгтэй тэнцүү бол суурь гэж нэрлэдэг. ортонормаль, мөн координатууд x 1 , x 2 , x 3 - тэгш өнцөгт.Ортонормаль суурийн суурь векторуудыг тэмдэглэнэ i, j, k.
Бид үүнийг сансарт гэж таамаглах болно Р 3 Декартын тэгш өнцөгт координатын зөв систем (0, i, j, k}.
Вектор бүтээгдэхүүн. вектор урлаг Авектор бүрт бвектор гэж нэрлэдэг вдараах гурван нөхцөлөөр тодорхойлогддог.
1. Векторын урт ввекторууд дээр баригдсан параллелограммын талбайтай тоон хувьд тэнцүү байна аТэгээд б,өөрөөр хэлбэл
в=
|a||b|нүгэл( а^б).
2. Вектор ввектор тус бүрт перпендикуляр байна аТэгээд б.
3. Векторууд а, бТэгээд в, энэ дарааллаар авбал баруун гурвалсан хэлбэрийг үүсгэнэ.
Вектор бүтээгдэхүүний хувьд втэмдэглэгээг танилцуулж байна c=[ab] эсвэл
c = a
× б.
Хэрэв векторууд аТэгээд б collinear, дараа нь нүгэл( a^b) = 0 ба [ ab] = 0, ялангуяа, [ аа] = 0. Ортын вектор бүтээгдэхүүн: [ ij]=к, [jk] = би, [ки]=j.
Хэрэв векторууд аТэгээд бүндэслэлд өгөгдсөн i, j, kкоординатууд а(a 1, a 2, a 3), б(b 1, b 2, b 3), дараа нь
Холимог ажил. Хэрэв хоёр векторын хөндлөн үржвэр бол АТэгээд бскалярыг гурав дахь вектороор үржүүлсэн в,тэгвэл гурван векторын ийм үржвэрийг гэнэ холимог бүтээгдэхүүнба тэмдгээр тэмдэглэнэ а МЭӨ.
Хэрэв векторууд а, бТэгээд вүндсэн дээр i, j, kтэдгээрийн координатаар тогтооно
а(a 1, a 2, a 3), б(b 1 , b 2 , b 3), в(c 1 , c 2 , c 3), дараа нь
.
Холимог бүтээгдэхүүн нь энгийн геометрийн тайлбартай байдаг - энэ нь өгөгдсөн гурван вектор дээр баригдсан параллелепипедийн эзэлхүүнтэй тэнцүү үнэмлэхүй утгаараа скаляр юм.
Хэрэв векторууд зөв гурвалсан бол тэдгээрийн холимог бүтээгдэхүүн нь заасан эзэлхүүнтэй тэнцүү эерэг тоо байна; хэрэв гурав a, b, c -тэгээд зүүн a b c<0 и V = - a b c, тиймээс V =|a b c|.
Нэгдүгээр бүлгийн бодлогод тулгарсан векторуудын координатыг зөв ортонормаль суурьтай харьцуулан өгсөн гэж үзнэ. Нэгж вектор вектор руу координат А,тэмдгээр тэмдэглэнэ АО. Тэмдэг r=ОММ цэгийн радиус вектороор a, AB эсвэл тэмдэгтээр тэмдэглэнэ|а|, | AB |векторуудын модулиудыг тэмдэглэв АТэгээд AB.
Жишээ 1.2. Векторуудын хоорондох өнцгийг ол а= 2м+4nТэгээд б= м-н, Хаана мТэгээд n-нэгж векторууд ба хоорондын өнцөг мТэгээд n 120 o-тай тэнцүү.
Шийдэл. Бидэнд байна: cos φ = ab/ab, ab=(2м+4n) (м-н) = 2м 2 - 4n 2 +2mn=
= 2 - 4+2cos120 o = - 2 + 2(-0.5) = -3; a = ; а 2 = (2м+4n) (2м+4n) =
= 4м 2 +16mn+16n 2 = 4+16(-0.5)+16=12 тул a = . b= ; б 2 =
= (м-н)(м-н) = м 2 -2mn+n 2 =
1-2(-0.5)+1 = 3 тул b = байна. Эцэст нь бидэнд байна: cosφ \u003d -1/2, φ \u003d 120 o.
Жишээ 1.3.Векторуудыг мэдэх AB(-3,-2.6) ба МЭӨ(-2,4,4), ABC гурвалжны AD өндрийг тооцоол.
Шийдэл. ABC гурвалжны талбайг S-ээр тэмдэглэвэл бид дараахь зүйлийг авна.
S = МЭӨ 1/2 МЭ. Дараа нь AD=2S/BC, BC== 
= 6,
S = 1/2| AB ×AC|.
AC=AB+BC, тэгэхээр вектор АСкоординаттай
.
Та векторууд болон тэдгээрийн үйлдлүүдийн талаар бүх зүйлийг сурахаасаа өмнө энгийн асуудлыг шийдэхийн тулд тааруулж үзээрэй. Таны аж ахуйн нэгжийн вектор ба шинэлэг чадварын вектор байдаг. Бизнес эрхлэх вектор нь таныг 1-р зорилгод, шинэлэг чадварын вектор нь 2-р зорилгод хүргэдэг. Тоглоомын дүрэм нь эдгээр хоёр векторын чиглэлд нэгэн зэрэг хөдөлж, хоёр зорилгод нэгэн зэрэг хүрч чадахгүй. Векторууд харилцан үйлчилдэг, эсвэл математикийн хувьд зарим үйлдлийг векторууд дээр гүйцэтгэдэг. Энэ үйлдлийн үр дүн нь "Үр дүн" вектор бөгөөд энэ нь таныг 3-р зорилгод хүргэдэг.
Одоо надад хэлээч: "Аж ахуйн нэгж" ба "Шинэлэг чадвар" векторуудын аль үйлдлийн үр дүн нь "Үр дүн" вектор вэ? Хэрэв та шууд хэлж чадахгүй бол сэтгэлээр унах хэрэггүй. Энэ хичээлийг судалснаар та энэ асуултанд хариулах боломжтой болно.
Дээр дурьдсанчлан вектор нь ямар нэгэн цэгээс ирдэг Атодорхой цэг хүртэл шулуун шугамаар Б. Тиймээс вектор бүр нь зөвхөн тоон утгатай байдаг - урт, бас физик, геометрийн чиглэлтэй байдаг. Эндээс векторын анхны, хамгийн энгийн тодорхойлолтыг гаргаж авсан. Тэгэхээр вектор гэдэг нь нэг цэгээс явж буй чиглэсэн сегмент юм Ацэг хүртэл Б. Үүнийг дараах байдлаар тэмдэглэв.
Тэгээд өөрөөр эхлэх вектор үйлдлүүд , бид векторын өөр нэг тодорхойлолттой танилцах хэрэгтэй.
Вектор гэдэг нь ямар нэгэн эхлэлийн цэгээс хүрэх цэгийн нэг төрлийн дүрслэл юм. Жишээлбэл, гурван хэмжээст векторыг ихэвчлэн ингэж бичдэг (x, y, z) . Энгийнээр хэлбэл, эдгээр тоо нь зорилгодоо хүрэхийн тулд гурван өөр чиглэлд хэр хол явах ёстойг илэрхийлдэг.
Вектор өгье. Хаана x = 3 (баруун гар нь баруун тийшээ заадаг) y = 1 (зүүн гар урагшаа заана) z = 5 (цэг дор дээшээ шат байдаг). Энэ өгөгдлөөс та баруун гараараа заасан чиглэлд 3 метр, зүүн гараараа зааж өгсөн чиглэлд 1 метр алхаж цэгийг олох болно, дараа нь шат таныг хүлээж, 5 метр авирч, эцэст нь олох болно. эцсийн цэг дээр өөрийгөө.
Бусад бүх нэр томъёо нь векторууд дээр янз бүрийн үйлдлүүд хийх, өөрөөр хэлбэл практик асуудлыг шийдвэрлэхэд шаардлагатай дээр дурдсан тайлбарын сайжруулалт юм. Ердийн вектор бодлого дээр тулгуурлан эдгээр илүү нарийн тодорхойлолтуудыг авч үзье.
Физик жишээнүүдвектор хэмжигдэхүүнүүд нь орон зайд хөдөлж буй материаллаг цэгийн шилжилт, энэ цэгийн хурд ба хурдатгал, түүнчлэн түүнд нөлөөлж буй хүч байж болно.
геометрийн векторхэлбэрээр хоёр хэмжээст болон гурван хэмжээст орон зайд дүрслэгдсэн чиглэсэн сегмент. Энэ бол эхлэл ба төгсгөлтэй сегмент юм.
Хэрэв Ань векторын эхлэл бөгөөд Бнь түүний төгсгөл бол векторыг тэмдэг эсвэл нэг жижиг үсгээр тэмдэглэнэ. Зураг дээр векторын төгсгөлийг сумаар зааж өгсөн болно (Зураг 1).
Урт(эсвэл модульГеометрийн векторын ) нь түүнийг үүсгэсэн сегментийн урт юм
Хоёр векторыг нэрлэдэг тэнцүү , хэрэв тэдгээрийг (чиглэлүүд давхцах үед) зэрэгцээ орчуулгаар нэгтгэх боломжтой бол, i.e. хэрэв тэдгээр нь параллель байвал ижил чиглэлд чиглүүлж, ижил урттай байна.
Физикийн хувьд үүнийг ихэвчлэн авч үздэг бэхлэгдсэн векторууд, хэрэглээний цэг, урт, чиглэлээр өгөгдсөн. Хэрэв векторын хэрэглээний цэг нь хамаагүй бол түүнийг орон зайн аль ч цэг рүү урт, чиглэлийг хадгалах замаар шилжүүлж болно. Энэ тохиолдолд векторыг дуудна үнэгүй. Бид зөвхөн авч үзэхийг зөвшөөрч байна үнэгүй векторууд.
Геометрийн векторууд дээрх шугаман үйлдлүүд
Векторыг тоогоор үржүүлэх
Вектор бүтээгдэхүүн тоо бүртВекторыг вектороос сунах ( at ) эсвэл багасах ( at ) үед олж авсан вектор гэж нэрлэх ба векторын чиглэл хэрэв байвал хадгалагдана, хэрэв байвал урвуу болно. (Зураг 2)
Тодорхойлолтоос харахад ба = векторууд үргэлж нэг буюу зэрэгцээ шулуун дээр байрлана. Ийм векторуудыг нэрлэдэг collinear. (Эдгээр векторууд параллель гэж бас хэлж болно, гэхдээ вектор алгебрт "конлинеар" гэж хэлдэг заншилтай.) Мөн эсрэгээр нь үнэн: хэрэв векторууд ба коллинеар байвал тэдгээр нь хамаарлаар холбогдоно.
Иймд тэгш байдал (1) нь хоёр векторын коллинеар байх нөхцөлийг илэрхийлдэг.
Вектор нэмэх ба хасах
Вектор нэмэхдээ үүнийг мэдэх хэрэгтэй нийлбэрвекторууд ба векторын эхлэл нь векторын төгсгөлд залгагдсан тохиолдолд эхлэл нь векторын эхлэлтэй , төгсгөл нь векторын төгсгөлтэй давхцах вектор гэж нэрлэгддэг . (Зураг 3)
Энэ тодорхойлолтыг дурын хязгаарлагдмал тооны векторуудад тарааж болно. Өгөгдсөн зайд оруулна уу nүнэгүй векторууд. Хэд хэдэн векторыг нэмэх үед тэдгээрийн нийлбэрийг хаалтын вектор болгон авдаг бөгөөд эхлэл нь эхний векторын эхлэлтэй, төгсгөл нь сүүлчийн векторын төгсгөлтэй давхцдаг. Өөрөөр хэлбэл, векторын эхлэлийг векторын төгсгөлд, векторын эхлэлийг векторын төгсгөлд хавсаргасан гэх мэт. эцэст нь векторын төгсгөл хүртэл - векторын эхлэл, дараа нь эдгээр векторуудын нийлбэр нь хаалтын вектор болно. 
, эхлэл нь эхний векторын эхлэлтэй , төгсгөл нь сүүлчийн векторын төгсгөлтэй давхцаж байгаа . (Зураг 4)
Нэр томьёог векторын бүрэлдэхүүн хэсэг гэж нэрлэдэг бөгөөд томъёолсон дүрэм нь олон өнцөгт дүрэм. Энэ олон өнцөгт хавтгай биш байж болно.
Векторыг -1 тоогоор үржүүлэхэд эсрэг вектор гарна. Векторууд нь ижил урттай, эсрэг чиглэлтэй байна. Тэдний нийлбэр өгдөг тэг вектор, урт нь тэг байна. Тэг векторын чиглэл тодорхойлогдоогүй байна.
Вектор алгебрийн хувьд хасах үйлдлийг тусад нь авч үзэх шаардлагагүй: вектороос векторыг хасах нь вектор руу эсрэг векторыг нэмэх гэсэн үг юм. 
Жишээ 1Илэрхийлэлийг хялбарчлах:
.
,
өөрөөр хэлбэл векторыг олон гишүүнтийн нэгэн адил тоогоор нэмж, үржүүлж болно (ялангуяа илэрхийллийг хялбарчлах бодлого). Ихэвчлэн векторуудын үржвэрийг тооцоолохын өмнө шугаман ижил төстэй илэрхийллийг векторуудтай хялбарчлах хэрэгцээ гарч ирдэг.
Жишээ 2Векторууд ба ABCD параллелограммын диагональ болдог (Зураг 4а). Энэ параллелограммын талууд болох , , ба , векторуудыг болон томъёогоор илэрхийл.
Шийдэл. Параллелограммын диагональуудын огтлолцлын цэг нь диагональ бүрийг хоёр хуваадаг. Асуудлын нөхцөлд шаардагдах векторуудын уртыг хүссэнтэй гурвалжин үүсгэх векторуудын нийлбэрийн тал, эсвэл зөрүүний тал хувь (диагональ болох векторын чиглэлээс хамаарч) олно. эсвэл сүүлийн тохиолдлын адил нийлбэрийн хагасыг хасах тэмдгээр авна. Үр дүн нь асуудлын нөхцөлд шаардлагатай векторууд юм.
Та энэ хичээлийн эхэнд "Аж ахуйн нэгж", "Шинэлэг чадвар" векторуудын тухай асуултад зөв хариулсан гэж үзэх бүх үндэслэл бий. Зөв хариулт: эдгээр векторууд нэмэх үйлдэлд хамрагдана.
Вектор дээрх асуудлыг бие даан шийдэж, дараа нь шийдлүүдийг хар
Векторуудын нийлбэрийн уртыг хэрхэн олох вэ?
Энэ асуудал нь тригонометрийн шинж чанарыг ашиглахтай холбоотой тул векторуудтай ажиллахад онцгой байр суурь эзэлдэг. Танд дараахтай адил даалгавар байна гэж бодъё.
Векторуудын уртыг өгсөн 
ба эдгээр векторуудын нийлбэрийн урт . Эдгээр векторуудын зөрүүний уртыг ол.
Энэ болон бусад ижил төстэй асуудлын шийдэл, тэдгээрийг хэрхэн шийдвэрлэх талаархи тайлбар - хичээл дээр " Вектор нэмэх: векторуудын нийлбэрийн урт ба косинусын теорем ".
Мөн та ийм асуудлын шийдлийг шалгаж болно Онлайн тооцоолуур "Гурвалжны үл мэдэгдэх тал (вектор нэмэх ба косинусын теорем)" .
Векторуудын бүтээгдэхүүн хаана байдаг вэ?
Векторын үржвэрүүд нь шугаман үйлдлүүд биш бөгөөд тусад нь авч үздэг. Мөн бид "Векторуудын цэгийн үржвэр", "Векторын вектор ба холимог бүтээгдэхүүн" гэсэн хичээлүүдтэй.
Векторын тэнхлэг дээрх проекц
Векторын тэнхлэг дээрх проекц нь төлөвлөсөн векторын урт ба вектор ба тэнхлэгийн хоорондох өнцгийн косинусын үржвэртэй тэнцүү байна.
Мэдэгдэж байгаагаар цэгийн төсөөлөл Ашугам (хавтгай) дээр энэ цэгээс шулуун (хавтгай) руу унасан перпендикулярын суурь байна.
- дурын вектор (Зураг 5), ба түүний эхлэлийн проекц (цэг А) ба төгсгөл (цэг Б) тэнхлэг бүрт л. (Цэгийн проекцийг бүтээх А) цэгээр шууд зур Ашулуунтай перпендикуляр хавтгай. Шугаман ба хавтгайн огтлолцол нь шаардлагатай проекцийг тодорхойлно.
Векторын бүрэлдэхүүн хэсэг l тэнхлэг дээрЭнэ тэнхлэг дээр байрлах ийм вектор гэж нэрлэгддэг бөгөөд түүний эхлэл нь эхлэлийн проекц, төгсгөл нь векторын төгсгөлийн проекцтой давхцдаг.
Векторын тэнхлэг дээрх проекц лдугаар дуудсан
,
бүрэлдэхүүн хэсгийн чиглэл нь тэнхлэгийн чиглэлтэй давхцаж байвал нэмэх тэмдгээр авсан энэ тэнхлэг дээрх бүрэлдэхүүн векторын урттай тэнцүү. л, хэрэв эдгээр чиглэлүүд эсрэг байвал хасах тэмдэгтэй.
Тэнхлэг дээрх вектор проекцын үндсэн шинж чанарууд:
1. Нэг тэнхлэг дээрх тэнцүү векторуудын проекцууд хоорондоо тэнцүү байна.
2. Векторыг тоогоор үржүүлэхэд проекцийг нь ижил тоогоор үржүүлнэ.
3. Аль ч тэнхлэг дээрх векторуудын нийлбэрийн проекц нь векторуудын гишүүнчлэлийн ижил тэнхлэг дээрх проекцуудын нийлбэртэй тэнцүү байна.
4. Векторын тэнхлэг дээрх проекц нь проекцолсон векторын урт ба вектор ба тэнхлэгийн хоорондох өнцгийн косинусын үржвэртэй тэнцүү байна.
.
Шийдэл. Векторуудыг тэнхлэгт проекц хийцгээе лдээрх онолын лавлагаанд тодорхойлсон. Зураг 5a-аас харахад векторуудын нийлбэрийн проекц нь векторуудын проекцын нийлбэртэй тэнцүү байна. Бид эдгээр төсөөллийг тооцоолно:
Бид векторуудын нийлбэрийн эцсийн проекцийг олно.
Орон зай дахь тэгш өнцөгт декартын координатын системтэй векторын хамаарал
-тай танилцах Сансар огторгуй дахь тэгш өнцөгт декартын координатын системийг холбогдох хичээл дээр авч үзсэн, шинэ цонхонд нээх нь дээр.
Координатын тэнхлэгүүдийн дараалсан системд 0xyzтэнхлэг Үхэрдуудсан x тэнхлэг, тэнхлэг 0 жил – у тэнхлэг, болон тэнхлэг 0z – тэнхлэгийг ашиглах.
дурын цэгтэй Мсансрын зангиа вектор
дуудсан радиус вектороноо Мкоординатын тэнхлэг тус бүр дээр проекц хийнэ. Харгалзах төсөөллийн утгыг тэмдэглэе.
Тоонууд x, y, zдуудсан М цэгийн координат, тус тус абсцисса, ординатТэгээд applique, мөн тоонуудын эрэмблэгдсэн цэг хэлбэрээр бичигдэнэ: M(x; y; z)(Зураг 6).
Чиглэл нь тэнхлэгийн чиглэлтэй давхцаж буй нэгж урттай векторыг нэрлэнэ нэгж вектор(эсвэл ортом) тэнхлэгүүд. -ээр тэмдэглээрэй
Үүний дагуу координатын тэнхлэгүүдийн нэгж векторууд Үхэр, Өө, Оз
Теорем.Аливаа векторыг координатын тэнхлэгүүдийн нэгж векторуудад задалж болно.
(2)
Тэгш байдлыг (2) координатын тэнхлэгүүдийн дагуу векторын тэлэлт гэж нэрлэдэг. Энэ тэлэлтийн коэффициентүүд нь координатын тэнхлэгүүд дээрх векторын проекцууд юм. Тиймээс координатын тэнхлэгүүдийн дагуух векторын тэлэлтийн коэффициентүүд (2) нь векторын координатууд болно.
Сансар огторгуйд тодорхой координатын системийг сонгосны дараа вектор ба түүний координатын гурав дахин бие биенээ өвөрмөц байдлаар тодорхойлдог тул векторыг хэлбэрээр бичиж болно.
(2) ба (3) хэлбэрийн вектор дүрслэл нь ижил байна.
Координат дахь коллинеар векторуудын нөхцөл
Өмнө дурьдсанчлан, векторууд хамааралтай бол тэдгээрийг коллинеар гэж нэрлэдэг
Векторуудыг үзье 
. Хэрэв векторуудын координат нь хамаарлаар хамааралтай бол эдгээр векторууд коллинеар байна
,
өөрөөр хэлбэл векторуудын координатууд пропорциональ байна.
Жишээ 6Өгөгдсөн векторууд 
. Эдгээр векторууд хоорондоо уялдаатай байна уу?
Шийдэл. Эдгээр векторуудын координатын харьцааг олж мэдье.
.
Векторуудын координатууд нь пропорциональ тул векторууд нь коллинеар, эсвэл ижилхэн нь параллель байна.
Векторын урт ба чиглэлийн косинусууд
Координатын тэнхлэгүүдийн харилцан перпендикуляр байдлаас шалтгаалан векторын урт
векторууд дээр баригдсан тэгш өнцөгт параллелепипедийн диагоналын урттай тэнцүү байна
тэгш эрхээр илэрхийлэгдэнэ
(4)
Вектор нь хоёр цэгийг (эхлэл ба төгсгөл) зааж өгснөөр бүрэн тодорхойлогддог тул векторын координатыг эдгээр цэгүүдийн координатаар илэрхийлж болно.
Өгөгдсөн координатын систем дэх векторын эхлэл цэг дээр байг
мөн төгсгөл нь цэг дээр байна
Тэгш эрхээс
Үүнийг дагадаг
эсвэл координат хэлбэрээр
Тиймээс, векторын координатууд нь векторын төгсгөл ба эхлэлийн ижил нэртэй координатын зөрүүтэй тэнцүү байна. . Энэ тохиолдолд томъёо (4) хэлбэрийг авна
Векторын чиглэлийг тодорхойлно чиглэлийн косинусууд . Эдгээр нь векторын тэнхлэгүүдээр хийдэг өнцгийн косинусууд юм Үхэр, ӨөТэгээд Оз. Эдгээр өнцгийг тус тусад нь тэмдэглэе α , β Тэгээд γ . Дараа нь эдгээр өнцгийн косинусыг томъёогоор олж болно
Векторын чиглэлийн косинусууд нь мөн векторын векторын координатууд бөгөөд ингэснээр векторын вектор юм
.
Вектор векторын урт нь нэг нэгжтэй тэнцүү байна гэж үзвэл, өөрөөр хэлбэл,
,
Бид чиглэлийн косинусуудын хувьд дараах тэгш байдлыг олж авна.
Жишээ 7Векторын уртыг ол x = (3; 0; 4).
Шийдэл. Векторын урт нь
Жишээ 8Өгөгдсөн оноо:
Эдгээр цэгүүд дээр баригдсан гурвалжин нь тэгш өнцөгт мөн эсэхийг олж мэд.
Шийдэл. Векторын уртын томъёог (6) ашиглан бид талуудын уртыг олж, тэдгээрийн хоёр нь тэнцүү эсэхийг олж мэдье.
Хоёр тэнцүү тал олдсон тул гурав дахь талын уртыг хайх шаардлагагүй бөгөөд өгөгдсөн гурвалжин нь ижил өнцөгт байна.
Жишээ 9Хэрэв векторын урт ба түүний чиглэлийн косинусуудыг ол 
.
Шийдэл. Векторын координатыг дараах байдлаар өгөв.
.
Векторын урт нь векторын координатын квадратуудын нийлбэрийн квадрат язгууртай тэнцүү байна.
.
Чиглэлийн косинусыг олох:
Вектор дээрх асуудлыг өөрөө шийдэж, дараа нь шийдлийг хар
Координат хэлбэрээр өгөгдсөн векторууд дээрх үйлдлүүд
Хоёр векторыг проекцоор нь өгье.
Эдгээр векторууд дээрх үйлдлүүдийг зааж өгье.
1. Нэмэлт:
эсвэл юу нь адилхан
(хоёр вектор нэмэхэд ижил нэртэй координатууд нэмэгддэг).
