Σωστό 6 τρίγωνο. Τι είναι ένα κανονικό εξάγωνο και ποιες εργασίες μπορούν να συσχετιστούν με αυτό; Από τη θεωρία στην πράξη

Η πιο διάσημη φιγούρα με περισσότερες από τέσσερις γωνίες είναι το κανονικό εξάγωνο. Στη γεωμετρία, χρησιμοποιείται συχνά σε προβλήματα. Και στη ζωή, αυτό ακριβώς έχουν οι κηρήθρες στο κόψιμο.

Σε τι διαφέρει από το λάθος;

Πρώτον, ένα εξάγωνο είναι ένα σχήμα με 6 κορυφές. Δεύτερον, μπορεί να είναι κυρτό ή κοίλο. Η πρώτη διαφέρει στο ότι τέσσερις κορυφές βρίσκονται στη μία πλευρά μιας ευθείας γραμμής που διασχίζεται από τις άλλες δύο.

Τρίτον, ένα κανονικό εξάγωνο χαρακτηρίζεται από το γεγονός ότι όλες οι πλευρές του είναι ίσες. Επιπλέον, κάθε γωνία του σχήματος έχει επίσης την ίδια αξία. Για να προσδιορίσετε το άθροισμα όλων των γωνιών του, θα χρειαστεί να χρησιμοποιήσετε τον τύπο: 180º * (n - 2). Εδώ n είναι ο αριθμός των κορυφών του σχήματος, δηλαδή 6. Ένας απλός υπολογισμός δίνει μια τιμή 720º. Άρα κάθε γωνία είναι 120 μοίρες.

Στις καθημερινές δραστηριότητες, ένα κανονικό εξάγωνο βρίσκεται σε μια νιφάδα χιονιού και ένα παξιμάδι. Οι χημικοί το βλέπουν ακόμη και στο μόριο του βενζολίου.

Ποιες ιδιότητες πρέπει να γνωρίζετε όταν επιλύετε προβλήματα;

Στα παραπάνω πρέπει να προστεθούν:

Οι διαγώνιοι του σχήματος, που σύρονται από το κέντρο, το χωρίζουν σε έξι τρίγωνα, τα οποία είναι ισόπλευρα.
η πλευρά ενός κανονικού εξαγώνου έχει μια τιμή που συμπίπτει με την ακτίνα του περιγεγραμμένου κύκλου γύρω του.
χρησιμοποιώντας ένα τέτοιο σχήμα, είναι δυνατό να γεμίσετε το επίπεδο και μεταξύ τους δεν θα υπάρχουν κενά και επικαλύψεις.

Εισήχθη η σημειογραφία

Παραδοσιακά, η πλευρά ενός κανονικού γεωμετρικού σχήματος συμβολίζεται με το λατινικό γράμμα "a". Για την επίλυση προβλημάτων απαιτούνται επίσης εμβαδόν και περίμετρος, αυτά είναι S και P, αντίστοιχα. Ένας κύκλος είναι εγγεγραμμένος σε ένα κανονικό εξάγωνο ή περιγεγραμμένος γύρω από αυτό. Στη συνέχεια εισάγονται τιμές για τις ακτίνες τους. Συμβολίζονται αντίστοιχα με τα γράμματα r και R.

Σε ορισμένους τύπους, εμφανίζεται μια εσωτερική γωνία, μια ημιπερίμετρος και ένα απόθεμα (το οποίο είναι κάθετο στο μέσο οποιασδήποτε πλευράς από το κέντρο του πολυγώνου). Για αυτούς χρησιμοποιούνται γράμματα: α, p, m.

Τύποι που περιγράφουν ένα σχήμα

Για να υπολογίσετε την ακτίνα ενός εγγεγραμμένου κύκλου, χρειάζεστε αυτό: r= (a * √3) / 2, και r = m. Δηλαδή, η ίδια φόρμουλα θα είναι και για το απόθεμα.

Εφόσον η περίμετρος ενός εξαγώνου είναι το άθροισμα όλων των πλευρών, θα καθοριστεί ως εξής: P = 6 * α. Δεδομένου ότι η πλευρά είναι ίση με την ακτίνα του περιγεγραμμένου κύκλου, για την περίμετρο υπάρχει ένας τέτοιος τύπος για ένα κανονικό εξάγωνο: P \u003d 6 * R. Από αυτόν που δίνεται για την ακτίνα του εγγεγραμμένου κύκλου, η σχέση μεταξύ ενός και το r προέρχεται. Τότε ο τύπος παίρνει την ακόλουθη μορφή: Р = 4 r * √3.

Για την περιοχή ενός κανονικού εξαγώνου, αυτό μπορεί να είναι χρήσιμο: S = p * r = (a 2 * 3 √3) / 2.

Καθήκοντα

Αρ. 1. Κατάσταση.Υπάρχει ένα κανονικό εξαγωνικό πρίσμα, κάθε άκρη του οποίου είναι ίσο με 4 εκ. Σε αυτό είναι εγγεγραμμένος ένας κύλινδρος, ο όγκος του οποίου πρέπει να προσδιοριστεί.

Λύση.Ο όγκος ενός κυλίνδρου ορίζεται ως το γινόμενο του εμβαδού της βάσης και του ύψους. Το τελευταίο συμπίπτει με την άκρη του πρίσματος. Και είναι ίσο με την πλευρά ενός κανονικού εξαγώνου. Δηλαδή και το ύψος του κυλίνδρου είναι 4 εκατοστά.

Για να μάθετε την περιοχή της βάσης του, πρέπει να υπολογίσετε την ακτίνα του κύκλου που εγγράφεται στο εξάγωνο. Ο τύπος για αυτό φαίνεται παραπάνω. Άρα r = 2√3 (cm). Στη συνέχεια, η περιοχή του κύκλου: S \u003d π * r 2 \u003d 3,14 * (2√3) 2 \u003d 37,68 (cm 2).

Απάντηση. V \u003d 150,72 cm 3.

Νο. 2. Κατάσταση.Να υπολογίσετε την ακτίνα ενός κύκλου που είναι εγγεγραμμένος σε κανονικό εξάγωνο. Είναι γνωστό ότι η πλευρά του είναι √3 εκ. Ποια θα είναι η περίμετρός του;

Λύση.Αυτή η εργασία απαιτεί τη χρήση δύο από τους παραπάνω τύπους. Επιπλέον, πρέπει να εφαρμοστούν χωρίς καν να τροποποιηθούν, απλώς αντικαταστήστε την τιμή της πλευράς και υπολογίστε.

Έτσι, η ακτίνα του εγγεγραμμένου κύκλου αποδεικνύεται 1,5 εκ. Για την περίμετρο, η ακόλουθη τιμή αποδεικνύεται σωστή: 6√3 cm.

Απάντηση. r = 1,5 cm, Р = 6√3 cm.

Αρ. 3. Κατάσταση.Η ακτίνα του περιγεγραμμένου κύκλου είναι 6 εκ. Τι τιμή θα έχει η πλευρά ενός κανονικού εξαγώνου σε αυτή την περίπτωση;

Λύση.Από τον τύπο για την ακτίνα ενός κύκλου εγγεγραμμένου σε ένα εξάγωνο, λαμβάνεται εύκολα αυτή με την οποία πρέπει να υπολογιστεί η πλευρά. Είναι σαφές ότι η ακτίνα πολλαπλασιάζεται επί δύο και διαιρείται με τη ρίζα του τριών. Είναι απαραίτητο να απαλλαγούμε από τον παραλογισμό στον παρονομαστή. Επομένως, το αποτέλεσμα των ενεργειών παίρνει την ακόλουθη μορφή: (12 √3) / (√3 * √3), δηλαδή 4√3.

Απάντηση. a = 4√3 cm.

Ξέρετε πώς μοιάζει ένα κανονικό εξάγωνο;
Αυτή η ερώτηση δεν έγινε τυχαία. Οι περισσότεροι μαθητές στην 11η τάξη δεν γνωρίζουν την απάντηση σε αυτό.

Κανονικό εξάγωνο είναι αυτό στο οποίο όλες οι πλευρές είναι ίσες και όλες οι γωνίες είναι επίσης ίσες..

Σιδερένιο παξιμάδι. Νιφάδα χιονιού. Ένα κελί από κηρήθρες στο οποίο ζουν μέλισσες. Μόριο βενζολίου. Τι κοινό έχουν αυτά τα αντικείμενα; - Το γεγονός ότι όλα έχουν κανονικό εξαγωνικό σχήμα.

Πολλοί μαθητές χάνονται όταν βλέπουν εργασίες για ένα κανονικό εξάγωνο και πιστεύουν ότι χρειάζονται κάποιες ειδικές φόρμουλες για την επίλυσή τους. Είναι έτσι?

Σχεδιάστε τις διαγώνιες ενός κανονικού εξαγώνου. Πήραμε έξι ισόπλευρα τρίγωνα.

Γνωρίζουμε ότι το εμβαδόν ενός ισόπλευρου τριγώνου είναι .

Τότε η περιοχή ενός κανονικού εξαγώνου είναι έξι φορές μεγαλύτερη.

Πού είναι η πλευρά ενός κανονικού εξαγώνου.

Σημειώστε ότι σε ένα κανονικό εξάγωνο, η απόσταση από το κέντρο του σε οποιαδήποτε από τις κορυφές είναι ίδια και ίση με την πλευρά του κανονικού εξαγώνου.

Αυτό σημαίνει ότι η ακτίνα ενός κύκλου που περιβάλλεται γύρω από ένα κανονικό εξάγωνο είναι ίση με την πλευρά του.
Η ακτίνα ενός κύκλου που εγγράφεται σε ένα κανονικό εξάγωνο είναι εύκολο να βρεθεί.
Είναι ίσος.
Τώρα μπορείτε εύκολα να λύσετε τυχόν προβλήματα ΧΡΗΣΗΣ στα οποία εμφανίζεται ένα κανονικό εξάγωνο.

Βρείτε την ακτίνα ενός κύκλου εγγεγραμμένου σε κανονικό εξάγωνο με πλευρά .

Η ακτίνα ενός τέτοιου κύκλου είναι .

Απάντηση: .

Ποια είναι η πλευρά ενός κανονικού εξαγώνου εγγεγραμμένου σε κύκλο με ακτίνα 6;

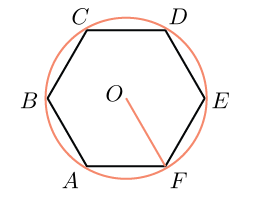
Γνωρίζουμε ότι η πλευρά ενός κανονικού εξαγώνου είναι ίση με την ακτίνα του κύκλου που περιβάλλεται γύρω από αυτό.

Κανονικό εξάγωνο είναι αυτό στο οποίο όλες οι πλευρές είναι ίσες και όλες οι γωνίες είναι επίσης ίσες..

Σχεδιάστε τις διαγώνιες ενός κανονικού εξαγώνου. Πήραμε έξι ισόπλευρα τρίγωνα.

Γνωρίζουμε ότι το εμβαδόν ενός ισόπλευρου τριγώνου είναι .

Τότε η περιοχή ενός κανονικού εξαγώνου είναι έξι φορές μεγαλύτερη.

Πού είναι η πλευρά ενός κανονικού εξαγώνου.

Βρείτε την ακτίνα ενός κύκλου εγγεγραμμένου σε κανονικό εξάγωνο με πλευρά .

Η ακτίνα ενός τέτοιου κύκλου είναι .

Απάντηση: .

Ποια είναι η πλευρά ενός κανονικού εξαγώνου εγγεγραμμένου σε κύκλο με ακτίνα 6;

Κατασκευή κανονικού εξαγώνου εγγεγραμμένου σε κύκλο.Η κατασκευή ενός εξαγώνου βασίζεται στο γεγονός ότι η πλευρά του είναι ίση με την ακτίνα του περιγεγραμμένου κύκλου. Επομένως, για την κατασκευή αρκεί να χωρίσετε τον κύκλο σε έξι ίσα μέρη και να συνδέσετε τα σημεία που βρέθηκαν μεταξύ τους (Εικ. 60, α).

Ένα κανονικό εξάγωνο μπορεί να κατασκευαστεί χρησιμοποιώντας ένα τετράγωνο Τ και ένα τετράγωνο 30Χ60°. Για να εκτελέσουμε αυτήν την κατασκευή, παίρνουμε την οριζόντια διάμετρο του κύκλου ως διχοτόμο των γωνιών 1 και 4 (Εικ. 60, β), κατασκευάζουμε τις πλευρές 1-6, 4-3, 4-5 και 7-2, μετά από τις οποίες ισοπαλία πλευρών 5-6 και 3-2.

Κατασκευή ισόπλευρου τριγώνου εγγεγραμμένου σε κύκλο. Οι κορυφές ενός τέτοιου τριγώνου μπορούν να κατασκευαστούν χρησιμοποιώντας μια πυξίδα και ένα τετράγωνο με γωνίες 30 και 60 ° ή μόνο μία πυξίδα.

Εξετάστε δύο τρόπους για να κατασκευάσετε ένα ισόπλευρο τρίγωνο εγγεγραμμένο σε κύκλο.

Πρώτος τρόπος(Εικ. 61, α) βασίζεται στο γεγονός ότι και οι τρεις γωνίες του τριγώνου 7, 2, 3 περιέχουν 60 ° η καθεμία και η κατακόρυφη γραμμή που διασχίζεται από το σημείο 7 είναι και το ύψος και η διχοτόμος της γωνίας 1. η γωνία 0-1- 2 είναι ίση με 30°, τότε για να βρείτε την πλευρά

1-2, αρκεί να χτίσετε μια γωνία 30 ° στο σημείο 1 και την πλευρά 0-1. Για να το κάνετε αυτό, ορίστε το τετράγωνο Τ και το τετράγωνο όπως φαίνεται στο σχήμα, σχεδιάστε μια γραμμή 1-2, η οποία θα είναι μία από τις πλευρές του επιθυμητού τριγώνου. Για να δημιουργήσετε την πλευρά 2-3, ρυθμίστε το τετράγωνο Τ στη θέση που φαίνεται από τις διακεκομμένες γραμμές και σχεδιάστε μια ευθεία γραμμή στο σημείο 2, η οποία θα ορίσει την τρίτη κορυφή του τριγώνου.

Δεύτερος τρόποςβασίζεται στο γεγονός ότι αν φτιάξετε ένα κανονικό εξάγωνο εγγεγραμμένο σε κύκλο και στη συνέχεια συνδέσετε τις κορυφές του μέσω ενός, θα έχετε ένα ισόπλευρο τρίγωνο.

Για να κατασκευάσουμε ένα τρίγωνο (Εικ. 61, β), σημειώνουμε ένα σημείο κορυφής 1 στη διάμετρο και σχεδιάζουμε μια διαμετρική γραμμή 1-4. Περαιτέρω, από το σημείο 4 με ακτίνα ίση με D / 2, περιγράφουμε το τόξο μέχρι να τέμνεται με τον κύκλο στα σημεία 3 και 2. Τα σημεία που θα προκύψουν θα είναι δύο άλλες κορυφές του επιθυμητού τριγώνου.

Κατασκευή τετραγώνου εγγεγραμμένου σε κύκλο. Αυτή η κατασκευή μπορεί να γίνει χρησιμοποιώντας ένα τετράγωνο και μια πυξίδα.

Η πρώτη μέθοδος βασίζεται στο γεγονός ότι οι διαγώνιοι του τετραγώνου τέμνονται στο κέντρο του περιγεγραμμένου κύκλου και έχουν κλίση προς τους άξονές του υπό γωνία 45°. Με βάση αυτό, εγκαθιστούμε ένα τετράγωνο Τ και ένα τετράγωνο με γωνίες 45 ° όπως φαίνεται στο Σχ. 62, α, και σημειώστε τα σημεία 1 και 3. Περαιτέρω, μέσα από αυτά τα σημεία, σχεδιάζουμε τις οριζόντιες πλευρές του τετραγώνου 4-1 και 3-2 με τη βοήθεια ενός τετραγώνου Τ. Στη συνέχεια, χρησιμοποιώντας ένα τετράγωνο Τ κατά μήκος του σκέλους του τετραγώνου, σχεδιάζουμε τις κάθετες πλευρές του τετραγώνου 1-2 και 4-3.

Η δεύτερη μέθοδος βασίζεται στο γεγονός ότι οι κορυφές του τετραγώνου διχοτομούν τα τόξα του κύκλου που περικλείονται μεταξύ των άκρων της διαμέτρου (Εικ. 62, β). Σημειώνουμε τα σημεία Α, Β και Γ στα άκρα δύο μεταξύ τους κάθετων διαμέτρων και από αυτά με ακτίνα y περιγράφουμε τα τόξα μέχρι να τέμνονται.

Περαιτέρω, μέσω των σημείων τομής των τόξων, σχεδιάζουμε βοηθητικές γραμμές, σημειωμένες στο σχήμα με συμπαγείς γραμμές. Τα σημεία τομής τους με τον κύκλο θα ορίσουν τις κορυφές 1 και 3. 4 και 2. Οι κορυφές του επιθυμητού τετραγώνου που λαμβάνονται με αυτόν τον τρόπο συνδέονται σε σειρά μεταξύ τους.

Κατασκευή κανονικού πενταγώνου εγγεγραμμένου σε κύκλο.

Για να εγγράψουμε ένα κανονικό πεντάγωνο σε κύκλο (Εικ. 63), κάνουμε τις παρακάτω κατασκευές.

Σημειώνουμε το σημείο 1 στον κύκλο και το παίρνουμε ως μια από τις κορυφές του πενταγώνου. Διαιρέστε το τμήμα AO στο μισό. Για να γίνει αυτό, με την ακτίνα AO από το σημείο Α, περιγράφουμε το τόξο στην τομή με τον κύκλο στα σημεία Μ και Β. Συνδέοντας αυτά τα σημεία με μια ευθεία γραμμή, παίρνουμε το σημείο Κ, το οποίο στη συνέχεια συνδέουμε στο σημείο 1. Με ακτίνα ίση με το τμήμα Α7, περιγράφουμε το τόξο από το σημείο Κ έως την τομή με τη διαμετρική γραμμή ΑΟ στο σημείο Η. Συνδέοντας το σημείο 1 με το σημείο Η, παίρνουμε την πλευρά του πενταγώνου. Στη συνέχεια, με ένα άνοιγμα πυξίδας ίσο με το τμήμα 1Η, που περιγράφει το τόξο από την κορυφή 1 έως την τομή με τον κύκλο, βρίσκουμε τις κορυφές 2 και 5. Έχοντας κάνει εγκοπές από τις κορυφές 2 και 5 με το ίδιο άνοιγμα πυξίδας, λαμβάνουμε το υπόλοιπο κορυφές 3 και 4. Συνδέουμε τα σημεία που βρέθηκαν διαδοχικά μεταξύ τους.

Κατασκευή κανονικού πενταγώνου δεδομένης της πλευράς του.

Για να κατασκευάσουμε ένα κανονικό πεντάγωνο κατά μήκος της δεδομένης πλευράς του (Εικ. 64), διαιρούμε το τμήμα ΑΒ σε έξι ίσα μέρη. Από τα σημεία Α και Β με ακτίνα ΑΒ περιγράφουμε τόξα, η τομή των οποίων θα δώσει το σημείο Κ. Μέσα από αυτό το σημείο και διαίρεση 3 στην ευθεία ΑΒ χαράσσουμε μια κάθετη γραμμή.

Παίρνουμε το σημείο 1-κορυφή του πενταγώνου. Στη συνέχεια, με ακτίνα ίση με ΑΒ, από το σημείο 1 περιγράφουμε το τόξο στη τομή με τα τόξα που σχεδιάστηκαν προηγουμένως από τα σημεία Α και Β. Τα σημεία τομής των τόξων καθορίζουν τις κορυφές του πενταγώνου 2 και 5. Συνδέουμε τα κορυφές σε σειρά μεταξύ τους.

Κατασκευή κανονικού επτάγωνου εγγεγραμμένου σε κύκλο.

Έστω ένας κύκλος διαμέτρου D. πρέπει να εγγράψετε ένα κανονικό επτάγωνο σε αυτό (Εικ. 65). Διαχωρίστε την κατακόρυφη διάμετρο του κύκλου σε επτά ίσα μέρη. Από το σημείο 7 με ακτίνα ίση με τη διάμετρο του κύκλου D, περιγράφουμε το τόξο μέχρι να τέμνεται με τη συνέχεια της οριζόντιας διαμέτρου στο σημείο F. Το σημείο F ονομάζεται πόλος του πολυγώνου. Λαμβάνοντας το σημείο VII ως μία από τις κορυφές του επτάγωνου, σχεδιάζουμε ακτίνες από τον πόλο F μέσω άρτιων διαιρέσεων της κατακόρυφης διαμέτρου, η τομή των οποίων με τον κύκλο θα καθορίσει τις κορυφές VI, V και IV του επτάγωνου. Για να λάβουμε κορυφές / - // - /// από τα σημεία IV, V και VI, σχεδιάζουμε οριζόντιες γραμμές μέχρι να τέμνονται με τον κύκλο. Συνδέουμε τις κορυφές που βρέθηκαν σε σειρά μεταξύ τους. Το επτάγωνο μπορεί να κατασκευαστεί αντλώντας ακτίνες από τον πόλο F και μέσα από περιττές διαιρέσεις της κατακόρυφης διαμέτρου.

Η παραπάνω μέθοδος είναι κατάλληλη για την κατασκευή κανονικών πολυγώνων με οποιοδήποτε αριθμό πλευρών.

Η διαίρεση ενός κύκλου σε οποιοδήποτε αριθμό ίσων μερών μπορεί επίσης να γίνει χρησιμοποιώντας τα δεδομένα στον Πίνακα. 2, το οποίο δείχνει τους συντελεστές που καθιστούν δυνατό τον προσδιορισμό των διαστάσεων των πλευρών των κανονικών εγγεγραμμένων πολυγώνων.

Το θέμα των πολυγώνων καλύπτεται στο σχολικό πρόγραμμα, αλλά δεν του δίνουν αρκετή σημασία. Εν τω μεταξύ, είναι ενδιαφέρον, και αυτό ισχύει ιδιαίτερα για ένα κανονικό εξάγωνο ή εξάγωνο - τελικά, πολλά φυσικά αντικείμενα έχουν αυτό το σχήμα. Αυτά περιλαμβάνουν κηρήθρες και άλλα. Αυτή η φόρμα εφαρμόζεται πολύ καλά στην πράξη.

Ορισμός και κατασκευή

Ένα κανονικό εξάγωνο είναι ένα επίπεδο σχήμα που έχει έξι πλευρές ίσες σε μήκος και τον ίδιο αριθμό ίσων γωνιών.

Αν θυμηθούμε τον τύπο για το άθροισμα των γωνιών ενός πολυγώνου

αποδεικνύεται ότι σε αυτό το σχήμα είναι ίσο με 720 °. Λοιπόν, δεδομένου ότι όλες οι γωνίες του σχήματος είναι ίσες, είναι εύκολο να υπολογίσουμε ότι καθεμία από αυτές είναι ίση με 120 °.

Το να σχεδιάσετε ένα εξάγωνο είναι πολύ απλό, το μόνο που χρειάζεστε είναι μια πυξίδα και ένα χάρακα.

Οι οδηγίες βήμα προς βήμα θα μοιάζουν με αυτό:

Εάν θέλετε, μπορείτε να κάνετε χωρίς γραμμή σχεδιάζοντας πέντε κύκλους ίσης ακτίνας.

Το σχήμα που προκύπτει θα είναι ένα κανονικό εξάγωνο, και αυτό μπορεί να αποδειχθεί παρακάτω.

Οι ιδιότητες είναι απλές και ενδιαφέρουσες

Για να κατανοήσουμε τις ιδιότητες ενός κανονικού εξαγώνου, είναι λογικό να το σπάσουμε σε έξι τρίγωνα:

Αυτό θα βοηθήσει στο μέλλον να εμφανίζει με μεγαλύτερη σαφήνεια τις ιδιότητές του, οι κυριότερες από τις οποίες είναι:

περιγεγραμμένη διάμετρος κύκλου.
διάμετρος του εγγεγραμμένου κύκλου.
τετράγωνο;
περίμετρος.

Ο περιγεγραμμένος κύκλος και η δυνατότητα κατασκευής

Είναι δυνατόν να περιγράψουμε έναν κύκλο γύρω από ένα εξάγωνο, και επιπλέον, μόνο ένα. Δεδομένου ότι αυτό το σχήμα είναι σωστό, μπορείτε να το κάνετε πολύ απλά: σχεδιάστε μια διχοτόμο από δύο γειτονικές γωνίες μέσα. Τέμνονται στο σημείο Ο, και μαζί με την μεταξύ τους πλευρά σχηματίζουν ένα τρίγωνο.

Οι γωνίες μεταξύ της πλευράς του εξαγώνου και των διχοτόμων θα είναι 60° η καθεμία, επομένως μπορούμε να πούμε με βεβαιότητα ότι ένα τρίγωνο, για παράδειγμα, το AOB, είναι ισοσκελές. Και δεδομένου ότι η τρίτη γωνία θα είναι επίσης ίση με 60 °, είναι επίσης ισόπλευρη. Από αυτό προκύπτει ότι τα τμήματα ΟΑ και ΟΒ είναι ίσα, πράγμα που σημαίνει ότι μπορούν να χρησιμεύσουν ως η ακτίνα του κύκλου.

Μετά από αυτό, μπορείτε να πάτε στην επόμενη πλευρά και επίσης να σχεδιάσετε μια διχοτόμο από τη γωνία στο σημείο C. Θα βγει ένα άλλο ισόπλευρο τρίγωνο και η πλευρά ΑΒ θα είναι κοινή με δύο ταυτόχρονα και το OS θα είναι η επόμενη ακτίνα μέσω της οποίας περνά ο ίδιος κύκλος. Θα υπάρχουν έξι τέτοια τρίγωνα συνολικά, και θα έχουν μια κοινή κορυφή στο σημείο Ο. Αποδεικνύεται ότι θα είναι δυνατό να περιγραφεί ο κύκλος, και είναι μόνο ένα, και η ακτίνα του είναι ίση με την πλευρά του εξαγώνου :

Αυτός είναι ο λόγος για τον οποίο είναι δυνατή η κατασκευή αυτής της φιγούρας με τη βοήθεια μιας πυξίδας και ενός χάρακα.

Λοιπόν, η περιοχή αυτού του κύκλου θα είναι τυπική:

Εγγεγραμμένος κύκλος

Το κέντρο του περιγεγραμμένου κύκλου συμπίπτει με το κέντρο του εγγεγραμμένου. Για να το επαληθεύσουμε αυτό, μπορούμε να σχεδιάσουμε κάθετες από το σημείο Ο προς τις πλευρές του εξαγώνου. Θα είναι τα ύψη εκείνων των τριγώνων που αποτελούν το εξάγωνο. Και σε ένα ισοσκελές τρίγωνο, το ύψος είναι το διάμεσο σε σχέση με την πλευρά στην οποία στηρίζεται. Έτσι, αυτό το ύψος δεν είναι παρά η κάθετη διχοτόμος, που είναι η ακτίνα του εγγεγραμμένου κύκλου.

Το ύψος ενός ισόπλευρου τριγώνου υπολογίζεται απλά:

h²=a²-(a/2)²= a²3/4, h=a(√3)/2

Και αφού R=a και r=h, αποδεικνύεται ότι

r=R(√3)/2.

Έτσι, ο εγγεγραμμένος κύκλος διέρχεται από τα κέντρα των πλευρών ενός κανονικού εξαγώνου.

Η περιοχή του θα είναι:

S=3πa²/4,

δηλαδή τα τρία τέταρτα αυτού που περιγράφεται.

Περίμετρος και εμβαδόν

Όλα είναι ξεκάθαρα με την περίμετρο, αυτό είναι το άθροισμα των μηκών των πλευρών:

Ρ=6α, ή P=6R

Αλλά το εμβαδόν θα είναι ίσο με το άθροισμα και των έξι τριγώνων στα οποία μπορεί να χωριστεί το εξάγωνο. Εφόσον το εμβαδόν ενός τριγώνου υπολογίζεται ως το μισό γινόμενο της βάσης και του ύψους, τότε:

S \u003d 6 (a / 2) (a (√3) / 2) \u003d 6a² (√3) / 4 \u003d 3a² (√3) / 2ή

S=3R²(√3)/2

Όσοι επιθυμούν να υπολογίσουν αυτό το εμβαδόν μέσω της ακτίνας του εγγεγραμμένου κύκλου μπορούν να γίνουν ως εξής:

S=3(2r/√3)²(√3)/2=r²(2√3)

Διασκεδαστικές κατασκευές

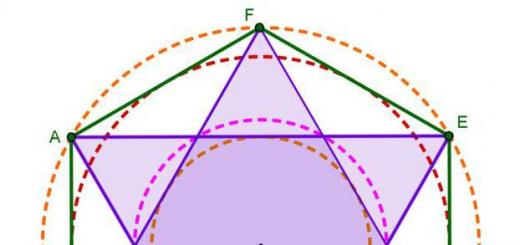
Ένα τρίγωνο μπορεί να εγγραφεί σε ένα εξάγωνο, οι πλευρές του οποίου θα συνδέουν τις κορυφές μέσω ενός:

Θα είναι δύο συνολικά και η επιβολή τους ο ένας στον άλλο θα δώσει το αστέρι του Δαβίδ. Κάθε ένα από αυτά τα τρίγωνα είναι ισόπλευρο. Αυτό είναι εύκολο να επαληθευτεί. Αν κοιτάξετε την πλευρά AC, τότε ανήκει σε δύο τρίγωνα ταυτόχρονα - BAC και AEC. Εάν στο πρώτο από αυτά AB \u003d BC, και η γωνία μεταξύ τους είναι 120 °, τότε καθένα από τα υπόλοιπα θα είναι 30 °. Από αυτό μπορούμε να βγάλουμε λογικά συμπεράσματα:

Το ύψος του ABC από την κορυφή Β θα είναι ίσο με τη μισή πλευρά του εξαγώνου, αφού sin30°=1/2. Όσοι επιθυμούν να το επαληθεύσουν αυτό μπορούν να συμβουλεύονται να υπολογίσουν ξανά σύμφωνα με το Πυθαγόρειο θεώρημα, ταιριάζει απόλυτα εδώ.
Η πλευρά AC θα είναι ίση με δύο ακτίνες του εγγεγραμμένου κύκλου, ο οποίος υπολογίζεται πάλι χρησιμοποιώντας το ίδιο θεώρημα. Δηλαδή AC=2(a(√3)/2)=a(√3).
Τα τρίγωνα ABC, CDE και AEF είναι ίσα σε δύο πλευρές και η μεταξύ τους γωνία και επομένως ακολουθεί η ισότητα των πλευρών AC, CE και EA.

Τέμνοντας μεταξύ τους, τα τρίγωνα σχηματίζουν ένα νέο εξάγωνο, και είναι επίσης κανονικό. Είναι εύκολο να αποδείξεις:

Έτσι, το σχήμα συναντά τα σημάδια ενός κανονικού εξαγώνου - έχει έξι ίσες πλευρές και γωνίες. Από την ισότητα των τριγώνων στις κορυφές, είναι εύκολο να συναχθεί το μήκος της πλευράς του νέου εξαγώνου:

d=а(√3)/3

Θα είναι επίσης η ακτίνα του κύκλου που περιγράφεται γύρω του. Η ακτίνα του εγγεγραμμένου θα είναι η μισή πλευρά του μεγάλου εξαγώνου, κάτι που αποδείχθηκε όταν λάβαμε υπόψη το τρίγωνο ΑΒΓ. Το ύψος του είναι ακριβώς το μισό της πλευράς, επομένως, το δεύτερο μισό είναι η ακτίνα του κύκλου που εγγράφεται στο μικρό εξάγωνο:

r2=а/2

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

Αποδεικνύεται ότι το εμβαδόν του εξαγώνου μέσα στο αστέρι του Δαβίδ είναι τρεις φορές μικρότερο από αυτό του μεγάλου στο οποίο είναι εγγεγραμμένο το αστέρι.

Από τη θεωρία στην πράξη

Οι ιδιότητες του εξαγώνου χρησιμοποιούνται πολύ ενεργά τόσο στη φύση όσο και σε διάφορους τομείς της ανθρώπινης δραστηριότητας. Πρώτα απ 'όλα, αυτό ισχύει για μπουλόνια και παξιμάδια - τα καπέλα του πρώτου και του δεύτερου δεν είναι τίποτα άλλο από ένα κανονικό εξάγωνο, αν δεν λάβετε υπόψη τις λοξοτομές. Το μέγεθος των κλειδιών αντιστοιχεί στη διάμετρο του εγγεγραμμένου κύκλου - δηλαδή, στην απόσταση μεταξύ των απέναντι όψεων.

Έχει βρει την εφαρμογή του και εξαγωνικά πλακάκια. Είναι πολύ λιγότερο κοινό από ένα τετράγωνο, αλλά είναι πιο βολικό να το τοποθετήσετε: τρία πλακάκια συναντώνται σε ένα σημείο, όχι τέσσερα. Οι συνθέσεις μπορεί να είναι πολύ ενδιαφέρουσες:

Παράγονται επίσης πλάκες από σκυρόδεμα.

Η επικράτηση του εξαγώνου στη φύση εξηγείται απλά. Έτσι, είναι πιο εύκολο να τοποθετήσετε κύκλους και μπάλες σφιχτά σε ένα αεροπλάνο εάν έχουν την ίδια διάμετρο. Εξαιτίας αυτού, οι κηρήθρες έχουν τέτοιο σχήμα.