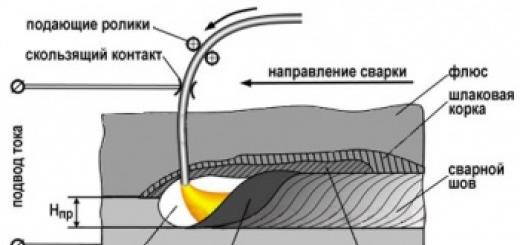
Sile, ki delujejo pravokotno na os žarka in se nahajajo v ravnini, ki poteka skozi to os, povzročijo deformacijo, imenovano prečni upogib. Če je ravnina delovanja omenjenih sil – glavno ravnino, potem nastane ravna (ravna) prečna krivina. V nasprotnem primeru se ovinek imenuje poševno prečno. Žarek, ki je podvržen pretežno upogibanju, se imenuje žarek 1 .

V bistvu je prečno upogibanje kombinacija čistega upogibanja in striga. V povezavi z ukrivljenostjo prečnih prerezov zaradi neenakomerne porazdelitve škarij po višini se postavlja vprašanje o možnosti uporabe formule normalne napetosti σ X, izpeljan za čisti upogib na podlagi hipoteze ravninskih prerezov.

1 Nosilec z enim razponom, ki ima na koncih eno cilindrično fiksno oporo in eno valjasto premično oporo v smeri osi nosilca, se imenuje preprosto. Imenuje se žarek, pri katerem je en konec vpet, drugi pa prost konzola. Imenuje se preprost žarek, ki ima enega ali dva dela, ki visijo nad nosilcem konzola.

Če so poleg tega odseki vzeti daleč od krajev, kjer se uporablja obremenitev (na razdalji, ki ni manjša od polovice višine odseka nosilca), se lahko domneva, kot v primeru čistega upogibanja, da vlakna ne pritiskajo druga na drugo. To pomeni, da vsako vlakno doživi enoosno napetost ali stiskanje.

Pod delovanjem porazdeljene obremenitve se bodo prečne sile v dveh sosednjih odsekih razlikovale za znesek, ki je enak qdx. Zato bo tudi ukrivljenost odsekov nekoliko drugačna. Poleg tega bodo vlakna med seboj pritiskala. Temeljita študija vprašanja kaže, da če je dolžina žarka l precej velik v primerjavi z njegovo višino h (l/ h> 5), potem tudi pri porazdeljeni obremenitvi ti dejavniki nimajo bistvenega vpliva na normalne napetosti v prerezu in zato v praktični izračuni morda ne bodo upoštevani.

a B C

riž. 10.5 Sl. 10.6

V odsekih pod koncentriranimi obremenitvami in blizu njih je porazdelitev σ X odstopa od linearnega zakona. To odstopanje, ki je lokalne narave in ga ne spremlja povečanje najvišjih napetosti (v najbolj zunanjih vlaknih), se v praksi običajno ne upošteva.

Tako s prečnim upogibanjem (v ravnini xy) normalne napetosti se izračunajo po formuli

σ X= – [M z(x)/Iz]l.

Če na odsek nosilca, ki je prost, narišemo dva sosednja preseka, bo prečna sila v obeh odsekih enaka, zato bo enaka tudi ukrivljenost odsekov. V tem primeru kateri koli kos vlaken ab(Sl. 10.5) se premakne na nov položaj a "b", brez dodatnega raztezka in torej brez spreminjanja vrednosti normalne napetosti.

Določimo tangencialne napetosti v prečnem prerezu preko njihovih parnih napetosti, ki delujejo v vzdolžnem prerezu nosilca.

Iz lesa izberite element dolžine dx(slika 10.7 a). Narišimo vodoravni odsek na daljavo pri od nevtralne osi z, razdelitev elementa na dva dela (sl. 10.7) in upoštevajte ravnotežje zgornjega dela, ki ima osnovo

premer b. V skladu z zakonom o združevanju tangencialnih napetosti so napetosti, ki delujejo v vzdolžnem prerezu, enake napetostim, ki delujejo v prečnem prerezu. Upoštevajoč to, ob predpostavki, da so strižne napetosti na mestu b enakomerno porazdeljena, z uporabo pogoja ΣХ = 0 dobimo:

N * - (N * +dN *)+

kjer je: N * rezultanta normalnih sil σ v levem preseku elementa dx znotraj "odrezanega" območja A * (slika 10.7 d):

kjer je: S = - statični moment "odrezanega" dela prečnega prereza (osenčeno območje na sliki 10.7 c). Zato lahko zapišemo:

Potem lahko zapišemo:

To formulo je v 19. stoletju pridobil ruski znanstvenik in inženir D.I. Zhuravsky in nosi njegovo ime. In čeprav je ta formula približna, saj povpreči napetost po širini odseka, se rezultati izračuna, dobljeni iz nje, dobro ujemajo z eksperimentalnimi podatki.

Za določitev strižnih napetosti v poljubni točki prečnega prereza, ki se nahaja na razdalji y od osi z, morate:

Iz diagrama določite velikost prečne sile Q, ki deluje v preseku;

Izračunajte vztrajnostni moment I z celotnega odseka;

Skozi to točko nariši ravnino, vzporedno z ravnino xz in določite širino odseka b;

Izračunajte statični moment odrezanega območja S glede na glavno središčno os z in nadomestite najdene vrednosti v formulo Zhuravsky.

Določimo kot primer tangencialne napetosti v pravokotnem prerezu (slika 10.6, c). Statični moment okoli osi z deli odseka nad vrstico 1-1, na katerih se določa napetost, bodo zapisani v obliki:

Spreminja se po zakonu kvadratne parabole. Širina odseka V za pravokotni nosilec je konstanten, potem bo zakon spremembe tangencialnih napetosti v odseku tudi paraboličen (sl. 10.6, c). Pri y = in y = − so tangencialne napetosti enake nič, na nevtralni osi pa z dosežejo največjo vrednost.

Za žarek krožnega prereza na nevtralni osi imamo.

Bend imenovana deformacija palice, ki jo spremlja sprememba ukrivljenosti njene osi. Palica, ki se upogne, se imenuje žarek.

Odvisno od načina obremenitve in načina pritrditve palice se lahko pojavijo težave. različne vrste upogibanje

Če se pod vplivom obremenitve v preseku palice pojavi samo upogibni moment, se imenuje upogib čisto.

Če v prečnih prerezih poleg upogibnih momentov nastanejo tudi prečne sile, se imenuje upogib prečni.

Če zunanje sile ležijo v ravnini, ki poteka skozi eno od glavnih središčnih osi preseka palice, se imenuje upogibanje preprosto oz stanovanje. V tem primeru breme in deformirana os ležita v isti ravnini (slika 1).

riž. 1

Da bi žarek lahko prevzel obremenitev v ravnini, ga je treba pritrditi z oporami: premičnimi, pritrjenimi ali zatesnjenimi.

Nosilec mora biti geometrijsko nespremenjen, pri čemer mora biti najmanjše število povezav 3. Primer geometrično spremenljivega sistema je prikazan na sliki 2a. Primer geometrično nespremenljivih sistemov je sl. 2b, c.

a B C)

V nosilcih potekajo reakcije, ki so določene iz pogojev statičnega ravnovesja. Reakcije v nosilcih so zunanje obremenitve.

Notranje upogibne sile

Palica, obremenjena s silami, ki so pravokotne na vzdolžno os žarka, doživlja ravno krivino(slika 3). V prerezih nastaneta dve notranji sili: strižna sila Qy in upogibni moment Mz.

Notranje sile so določene z metodo preseka. Na daljavo x od točke A Palica je razrezana na dva dela z ravnino, pravokotno na os X. Eden od delov žarka se zavrže. Interakcija delov nosilca se nadomesti z notranjimi silami: upogibni moment Mz in strižna sila Qy(slika 4).

Notranja prizadevanja Mz in Qy presek se določi iz ravnotežnih pogojev.

Za del je sestavljena enačba ravnotežja Z:

∑l = R A – P 1 – Q y = 0.

Potem Qy = R A – p1.

Zaključek. Prečna sila v katerem koli odseku nosilca je enaka algebraični vsoti vseh zunanjih sil, ki ležijo na eni strani prečnega prereza. Prečna sila velja za pozitivno, če vrti palico glede na točko prečnega prereza v smeri urinega kazalca.

∑M 0 = R A ∙ x – p 1 ∙ (x - a) – Mz = 0

Potem Mz = R A ∙ x – p 1 ∙ (x – a)

1. Določitev reakcij R A , R B ;

∑M A = p ∙ a – R B ∙ l = 0

R B =

∑M B = R A ∙ e – P ∙ a = 0

2. Izdelava diagramov v prvem delu 0 ≤ x 1 ≤ a

Q y = R A =; M z = R A ∙ x 1

x 1 = 0 M z (0) = 0

x 1 = a M z (a) =

3. Izdelava diagramov v drugem delu 0 ≤ x 2 ≤ b

Qy = - R B = - ; Mz = R B ∙ x 2 ; x 2 = 0 Mz(0) = 0 x 2 = bMz(b) =

Pri gradnji Mz pozitivne koordinate bodo odložene proti raztegnjenim vlaknom.

Preverjanje diagramov

1. Na diagramu Qy pretrganja lahko nastanejo samo na mestih, kjer delujejo zunanje sile in velikost preskoka mora ustrezati njihovi velikosti.

+ = = p

2. Na diagramu Mz Diskontinuitete nastanejo na mestih, kjer delujejo koncentrirani momenti in je velikost skoka enaka njihovi velikosti.

Diferencialne odvisnosti medM, Qinq

Med upogibnim momentom, strižno silo in intenzivnostjo porazdeljene obremenitve so bila vzpostavljena naslednja razmerja:

q = , Qy =

kjer je q intenzivnost porazdeljene obremenitve,

Preverjanje upogibne trdnosti nosilcev

Za oceno upogibne trdnosti palice in izbiro odseka žarka se uporabljajo pogoji trdnosti, ki temeljijo na normalnih napetostih.

Upogibni moment je rezultanta normalnih notranjih sil, porazdeljenih po preseku.

s = × l,

kjer je s normalna napetost na kateri koli točki prečnega prereza,

l– razdalja od težišča odseka do točke,

Mz– upogibni moment, ki deluje v preseku,

J z– osni vztrajnostni moment palice.

Za zagotovitev trdnosti se izračunajo največje napetosti, ki se pojavijo v točkah preseka, ki so najbolj oddaljene od težišča l = ymax

s max = × ymax,

= W z in s max = .

Potem ima pogoj trdnosti za normalne napetosti obliko:

s max = ≤ [s],

kjer je [s] dovoljena natezna napetost.

Upogibna deformacija sestoji iz ukrivljenosti osi ravne palice ali v spremembi začetne ukrivljenosti ravne palice (slika 6.1). Spoznajmo osnovne pojme, ki se uporabljajo pri obravnavanju upogibne deformacije.

Palice, ki se upognejo, se imenujejo tramovi.

čisto imenovano upogibanje, pri katerem je upogibni moment edini faktor notranje sile, ki nastane v prerezu nosilca.

Pogosteje se v prerezu palice poleg upogibnega momenta pojavi tudi prečna sila. Ta upogib se imenuje prečni.

Ravno (ravno) imenujemo upogib, ko ravnina delovanja upogibnega momenta v prerezu poteka skozi eno od glavnih središčnih osi prereza.

pri poševni ovinek ravnina delovanja upogibnega momenta seka prerez žarka vzdolž črte, ki ne sovpada z nobeno od glavnih središčnih osi prereza.

Študijo upogibne deformacije začnemo s primerom čistega ravninskega upogiba.

Normalne napetosti in deformacije med čistim upogibom.

Kot je bilo že omenjeno, je pri čistem ravninskem upogibu v prečnem prerezu od šestih faktorjev notranje sile le upogibni moment različen od nič (slika 6.1, c):

Poskusi, izvedeni na elastičnih modelih, kažejo, da če se na površino modela nanese mreža črt (slika 6.1, a), se s čistim upogibom deformira na naslednji način (slika 6.1, b):

a) vzdolžne črte so ukrivljene vzdolž oboda;

b) obrisi prerezov ostanejo ravni;

c) konturne črte odsekov se povsod sekajo z vzdolžnimi vlakni pod pravim kotom.

Na podlagi tega se lahko domneva, da pri čistem upogibanju ostanejo prečni prerezi nosilca ravni in se vrtijo tako, da ostanejo normalni na ukrivljeno os nosilca (ravni odseki v hipotezi o upogibanju).

riž. 6.1

Z merjenjem dolžine vzdolžnih črt (slika 6.1, b) lahko ugotovite, da se zgornja vlakna podaljšajo, ko se žarek upogne, spodnja pa se skrajšajo. Očitno je mogoče najti vlakna, katerih dolžina ostane nespremenjena. Niz vlaken, ki ne spremenijo svoje dolžine, ko je žarek upognjen, se imenuje nevtralna plast (n.s.). Nevtralna plast seka prečni prerez žarka v ravni črti, ki se imenuje odsek nevtralne črte (n.l.)..

Za izpeljavo formule, ki določa velikost normalnih napetosti, ki nastanejo v prečnem prerezu, upoštevajte odsek nosilca v deformiranem in nedeformiranem stanju (slika 6.2).

riž. 6.2

Z dvema infinitezimalnima presekoma izberemo element dolžine
. Pred deformacijo odseki, ki omejujejo element
, so bili vzporedni drug z drugim (slika 6.2, a), po deformaciji pa so se rahlo upognili in tvorili kot
. Dolžina vlaken, ki ležijo v nevtralni plasti, se pri upogibanju ne spremeni
. Polmer ukrivljenosti sledi nevtralne plasti na risalni ravnini označimo s črko . Določimo linearno deformacijo poljubnega vlakna
, ki se nahaja na daljavo iz nevtralne plasti.

Dolžina tega vlakna po deformaciji (dolžina loka
) je enako
. Glede na to, da so imela pred deformacijo vsa vlakna enako dolga
, ugotovimo, da je absolutni raztezek obravnavanega vlakna

Njegova relativna deformacija

To je očitno
, saj se dolžina vlakna, ki leži v nevtralni plasti, ni spremenila. Potem po zamenjavi
dobimo

(6.2)

Zato je relativna vzdolžna deformacija sorazmerna z oddaljenostjo vlakna od nevtralne osi.

Naj uvedemo predpostavko, da pri upogibanju vzdolžna vlakna ne pritiskajo druga na drugo. Pod to predpostavko se vsako vlakno deformira ločeno, pri čemer doživi preprosto napetost ali stiskanje, pri čemer
. ob upoštevanju (6.2)

, (6.3)

to pomeni, da so normalne napetosti neposredno sorazmerne z oddaljenostjo točk prečnega prereza od nevtralne osi.

Zamenjajmo odvisnost (6.3) v izraz za upogibni moment
v prerezu (6.1)

.

Spomnimo se, da je integral
predstavlja vztrajnostni moment preseka glede na os

.

(6.4)

Odvisnost (6.4) predstavlja Hookov zakon za upogib, saj povezuje deformacijo (ukrivljenost nevtralne plasti).
) s trenutkom, ki deluje v odseku. delo
se imenuje togost preseka med upogibanjem, N m 2.

Zamenjajmo (6.4) v (6.3)

(6.5)

To je zahtevana formula za določanje normalnih napetosti med čistim upogibanjem nosilca na kateri koli točki njegovega prečnega prereza.

Da bi ugotovili, kje v prečnem prerezu se nahaja nevtralna črta, v izraz za vzdolžno silo nadomestimo vrednost normalnih napetosti.
in upogibni moment

Zaradi
,

;

(6.6)

(6.7)

Enačba (6.6) kaže, da je os – nevtralna os prereza – poteka skozi težišče prereza.

Enakost (6.7) to pokaže in - glavne središčne osi prereza.

Po (6.5) je najvišja napetost dosežena v vlaknih, ki so najbolj oddaljena od nevtralne črte

Odnos predstavlja osni uporni moment preseka glede na njegovo središčno os , Pomeni

Pomen za najpreprostejše prereze naslednje:

Za pravokoten prerez

, (6.8)

Kje - stran odseka pravokotna na os ;

- stran odseka vzporedna z osjo ;

Za okrogel prerez

, (6.9)

Kje - premer krožnega preseka.

Trdnostni pogoj za normalne upogibne napetosti lahko zapišemo v obliki

(6.10)

Vse dobljene formule so bile pridobljene za primer čistega upogiba ravne palice. Delovanje prečne sile vodi v dejstvo, da hipoteze, na katerih temeljijo zaključki, izgubijo svojo moč. Vendar pa računska praksa kaže, da tudi pri prečnem upogibanju nosilcev in okvirjev, ko so v prerezu, poleg upogibnega momenta
obstaja tudi vzdolžna sila
in strižna sila , lahko uporabite formule, podane za čisto upogibanje. Napaka je nepomembna.

Ravno prečno upogibanje nosilcev. Notranje upogibne sile. Diferencialne odvisnosti notranjih sil. Pravila za preverjanje diagramov notranjih upogibnih sil. Normalne in strižne napetosti pri upogibanju. Izračun trdnosti na podlagi normalnih in tangencialnih napetosti.

10. ENOSTAVNE VRSTE UPORA. PLOŠČATI ZAVIJ

10.1. Splošni pojmi in definicije

Upogibanje je vrsta obremenitve, pri kateri je palica obremenjena z momenti v ravninah, ki potekajo skozi vzdolžno os palice.

Palica, ki se upogne, se imenuje tram (ali les). V prihodnje bomo obravnavali premočrtne nosilce, katerih presek ima vsaj eno simetrično os.

Upornost materialov delimo na ravno, poševno in kompleksno upogibanje.

Ravninski upogib je upogib, pri katerem vse sile, ki upogibajo nosilec, ležijo v eni od ravnin simetrije nosilca (v eni od glavnih ravnin).

Glavne vztrajnostne ravnine nosilca so ravnine, ki potekajo skozi glavne osi prerezov in geometrijsko os nosilca (x-os).

Poševni upogib je upogib, pri katerem obremenitve delujejo v eni ravnini, ki ne sovpada z glavnimi vztrajnostnimi ravninami.

Kompleksni upogib je upogib, pri katerem obremenitve delujejo v različnih (poljubnih) ravninah.

10.2. Določanje notranjih upogibnih sil

Oglejmo si dva tipična primera upogiba: v prvem je konzolni nosilec upognjen s koncentriranim momentom M o ; v drugem - s koncentrirano silo F.

Z metodo miselnih prerezov in sestavljanjem ravnotežnih enačb za odrezane dele nosilca določimo notranje sile v obeh primerih:

Preostale ravnotežne enačbe so očitno identično enake nič.

Tako v splošnem primeru ravninskega upogiba v prerezu nosilca od šestih notranjih sil nastaneta dve - upogibni moment M z in strižna sila Q y (ali pri upogibanju glede na drugo glavno os - upogibni moment M y in strižna sila Q z).

Poleg tega lahko v skladu z obravnavanima primeroma obremenitve ravninski upogib razdelimo na čisti in prečni.

Čisti upogib je ravninski upogib, pri katerem se v odsekih palice pojavi samo ena od šestih notranjih sil - upogibni moment (glej prvi primer).

Prečni zavoj– upogib, pri katerem v odsekih palice poleg notranjega upogibnega momenta nastane tudi prečna sila (glej drugi primer).

Strogo gledano, preproste vrste odpornosti vključujejo samo čisto upogibanje; prečni upogib običajno uvrščamo med enostavne vrste upora, saj se v večini primerov (pri dovolj dolgih nosilcih) pri izračunu trdnosti lahko zanemari učinek prečne sile.

Pri določanju notranjih naporov se bomo držali naslednjega pravila znakov:

1) prečna sila Q y se šteje za pozitivno, če teži k vrtenju zadevnega žarkovnega elementa v smeri urinega kazalca;

2) upogibni moment M z se šteje za pozitivno, če se pri upogibanju nosilnega elementa zgornja vlakna elementa stisnejo in spodnja vlakna raztegnejo (krovno pravilo).

Tako bomo zgradili rešitev problema določanja notranjih sil med upogibanjem po naslednjem načrtu: 1) na prvi stopnji, ob upoštevanju ravnotežnih pogojev konstrukcije kot celote, po potrebi določimo neznane reakcije podpor (upoštevajte, da so lahko za konzolni nosilec reakcije v vgradnji in ne najdene, če upoštevamo nosilec s prostega konca); 2) na drugi stopnji izberemo značilne odseke žarka, pri čemer kot meje odsekov vzamemo točke uporabe sil, točke spremembe oblike ali velikosti žarka, točke pritrditve žarka; 3) na tretji stopnji določimo notranje sile v odsekih žarka ob upoštevanju pogojev ravnovesja elementov žarka v vsakem odseku.

10.3. Diferencialne odvisnosti pri upogibanju

Vzpostavimo nekaj razmerij med notranjimi silami in zunanjimi obremenitvami pri upogibanju ter značilnosti diagramov Q in M, katerih poznavanje bo olajšalo gradnjo diagramov in nam omogočilo nadzor nad njihovo pravilnostjo. Za lažje zapisovanje bomo označili: M ≡ M z, Q ≡ Q y.

Izberimo majhen element dx v odseku nosilca s poljubno obremenitvijo na mestu, kjer ni zgoščenih sil in momentov. Ker je celoten nosilec v ravnovesju, bo tudi element dx v ravnovesju pod delovanjem strižnih sil, upogibnih momentov in zunanje obremenitve, ki delujejo nanj. Ker se Q in M ​​na splošno spreminjata vzdolž osi žarka, se bodo v odsekih elementa dx pojavile prečne sile Q in Q +dQ ter upogibni momenti M in M ​​+dM. Iz pogoja ravnovesja izbranega elementa dobimo

∑ F y = 0 Q + q dx − (Q + dQ) = 0;

∑ M 0 = 0 M + Q dx + q dx dx 2 − (M + dM ) = 0.

Iz druge enačbe, pri čemer zanemarimo izraz q dx (dx /2) kot infinitezimalno količino drugega reda, najdemo

Relacije (10.1), (10.2) in (10.3) imenujemo diferencialne odvisnosti D.I. Zhuravsky med upogibanjem.

Analiza zgornjih diferencialnih odvisnosti med upogibanjem nam omogoča, da določimo nekatere značilnosti (pravila) za izdelavo diagramov upogibnih momentov in prečnih sil:

a – na območjih, kjer ni porazdeljene obremenitve q, so diagrami Q omejeni na ravne črte, vzporedne s podlago, diagrami M pa na nagnjene ravne črte;

b – v območjih, kjer na nosilec deluje porazdeljena obremenitev q, so diagrami Q omejeni z nagnjenimi ravnimi črtami, diagrami M pa s kvadratnimi parabolami. Poleg tega, če sestavimo diagram M "na raztegnjenem vlaknu", potem je konveksnost pa-

delo bo usmerjeno v smeri delovanja q, ekstrem pa bo v odseku, kjer diagram Q seka osnovno črto;

c – v odsekih, kjer na nosilec deluje koncentrirana sila, bodo na diagramu Q skoki po velikosti in v smeri te sile, na diagramu M pa pregibi, konica je usmerjena v smeri delovanja ta sila; d – v odsekih, kjer je na žarek na epi-

ne bo sprememb re Q, na diagramu M pa bodo skoki za vrednost tega trenutka; d – v območjih, kjer je Q >0, v trenutku, ko se M poveča, in v območjih, kjer je Q<0, момент М убывает (см. рисунки а–г).

10.4. Normalne napetosti med čistim upogibom ravnega nosilca

Oglejmo si primer čistega ravninskega upogiba nosilca in izpeljimo formulo za določanje normalnih napetosti za ta primer. Upoštevajte, da je v teoriji elastičnosti mogoče dobiti natančno odvisnost normalnih napetosti med čistim upogibanjem, če pa se ta problem reši z metodami odpornosti materialov, je treba uvesti nekaj predpostavk.

Obstajajo tri takšne hipoteze za upogibanje:

a – hipoteza ravninskih prerezov (Bernoullijeva hipoteza)

– prerezi, ki so ravni pred deformacijo, ostanejo ravni po deformaciji, vendar se vrtijo le glede na določeno črto, ki se imenuje nevtralna os prereza nosilca. V tem primeru se bodo vlakna žarka, ki ležijo na eni strani nevtralne osi, raztegnila, na drugi pa stisnila; vlakna, ki ležijo na nevtralni osi, ne spremenijo svoje dolžine;

b – hipoteza o nespremenljivosti normalnih napetosti

niy – napetosti, ki delujejo na enaki razdalji y od nevtralne osi, so konstantne po širini nosilca;

c – hipoteza o odsotnosti bočnih pritiskov – ko-

Siva vzdolžna vlakna ne pritiskajo druga na drugo.

Ravni ovinek. Ravninsko prečno upogibanje Izdelava diagramov notranjih faktorjev sile za nosilce Izdelava diagramov Q in M ​​z uporabo enačb Izdelava diagramov Q in M ​​z uporabo karakterističnih prerezov (točk) Izračuni trdnosti za direktni upogib nosilcev Glavne napetosti pri upogibanju. Popolna kontrola upogibnih središč. Koncepti deformacije nosilcev in pogoji za njihovo togost Diferencialna enačba ukrivljene osi nosilca Metoda neposredne integracije Primeri določanja pomikov v nosilcih z metodo neposredne integracije Fizični pomen integracijskih konstant Metoda začetnih parametrov (univerzalna enačba ukrivljene os žarka). Primeri določanja pomikov v nosilcu z metodo začetnih parametrov. Določanje pomikov po Mohrovi metodi. Pravilo A.K. Vereščagin. Izračun Mohrovega integrala po pravilu A.K. Vereshchagina Primeri določanja pomikov z uporabo Mohrovega integrala Bibliografija Direktno upogibanje. Ravni prečni zavoj. 1.1. Konstruiranje diagramov notranjih faktorjev sile za nosilce Neposredni upogib je vrsta deformacije, pri kateri se v presekih palice pojavita dva faktorja notranje sile: upogibni moment in prečna sila. V določenem primeru je lahko strižna sila enaka nič, potem se upogib imenuje čisti. Pri ravnem prečnem upogibanju se vse sile nahajajo v eni od glavnih vztrajnostnih ravnin palice in pravokotno na njeno vzdolžno os, momenti pa se nahajajo v isti ravnini (sl. 1.1, a, b). riž. 1.1 Prečna sila v poljubnem prerezu nosilca je številčno enaka algebraični vsoti projekcij na normalo na os nosilca vseh zunanjih sil, ki delujejo na eni strani obravnavanega odseka. Prečna sila v m-n odseku žarka (sl. 1.2, a) se šteje za pozitivno, če je rezultanta zunanjih sil na levi strani odseka usmerjena navzgor, na desno - navzdol in negativna - v nasprotnem primeru (slika 1.2, b). riž. 1.2 Pri izračunu prečne sile v danem odseku se zunanje sile, ki ležijo levo od odseka, vzamejo z znakom plus, če so usmerjene navzgor, in z znakom minus, če so usmerjene navzdol. Za desno stran žarka - obratno. 5 Upogibni moment v poljubnem prerezu nosilca je številčno enak algebraični vsoti momentov okoli središčne osi z odseka vseh zunanjih sil, ki delujejo na eni strani obravnavanega odseka. Upogibni moment v odseku m-n žarka (sl. 1.3, a) se šteje za pozitivnega, če je rezultantni moment zunanjih sil na levi strani odseka usmerjen v smeri urinega kazalca, na desni - v nasprotni smeri urinega kazalca in negativen - v nasprotni smeri. ohišje (sl. 1.3, b). riž. 1.3 Pri izračunu upogibnega momenta v določenem odseku se momenti zunanjih sil, ki ležijo levo od odseka, štejejo za pozitivne, če so usmerjeni v smeri urinega kazalca. Za desno stran žarka - obratno. Primerno je določiti znak upogibnega momenta glede na naravo deformacije žarka. Upogibni moment se šteje za pozitivnega, če se v obravnavanem odseku odrezani del žarka upogne konveksno navzdol, to je, da so spodnja vlakna raztegnjena. V nasprotnem primeru je upogibni moment v preseku negativen. Med upogibnim momentom M, strižno silo Q in intenzivnostjo obremenitve q obstajajo diferencialna razmerja. 1. Prvi odvod strižne sile vzdolž abscise preseka je enak intenzivnosti porazdeljene obremenitve, tj. . (1.1) 2. Prvi odvod upogibnega momenta vzdolž abscise preseka je enak prečni sili, tj. (1.2) 3. Drugi odvod glede na absciso preseka je enak jakosti porazdeljene obremenitve, tj. (1.3) Porazdeljeno obremenitev, usmerjeno navzgor, štejemo za pozitivno. Iz diferencialnih razmerij med M, Q, q izhajajo številni pomembni zaključki: 1. Če je na prerezu nosilca: a) prečna sila pozitivna, se upogibni moment poveča; b) strižna sila je negativna, potem se upogibni moment zmanjša; c) prečna sila je nič, potem ima upogibni moment konstantno vrednost (čisti upogib); 6 d) prečna sila prehaja skozi nič, spreminja predznak iz plusa v minus, max M M, v nasprotnem primeru M Mmin. 2. Če na odseku nosilca ni porazdeljene obremenitve, je prečna sila konstantna, upogibni moment pa se spreminja po linearnem zakonu. 3. Če je na odseku nosilca enakomerno porazdeljena obremenitev, se prečna sila spremeni po linearnem zakonu in upogibni moment - po zakonu kvadratne parabole, konveksno obrnjene v smeri obremenitve ( v primeru konstruiranja diagrama M s strani raztegnjenih vlaken). 4. Na odseku pod zgoščeno silo ima diagram Q skok (za velikost sile), diagram M ima pregib v smeri sile. 5. Na odseku, kjer je uporabljen koncentrirani moment, ima diagram M skok, ki je enak vrednosti tega momenta. To se ne odraža v diagramu Q. Ko so nosilci obremenjeni s kompleksno obremenitvijo, se izrišejo diagrami prečnih sil Q in upogibnih momentov M Diagram Q(M) je graf, ki prikazuje zakon spremembe prečne sile (upogibnega momenta) po dolžini nosilca. Na podlagi analize diagramov M in Q so določeni nevarni odseki nosilca. Pozitivne ordinate diagrama Q so položene navzgor, negativne ordinate pa so položene navzdol od osnovne črte, narisane vzporedno z vzdolžno osjo žarka. Pozitivne ordinate M diagrama so položene navzdol, negativne ordinate pa navzgor, kar pomeni, da je M diagram sestavljen s strani raztegnjenih vlaken. Konstrukcijo diagramov Q in M ​​za nosilce je treba začeti z določitvijo reakcij podpore. Pri nosilcu z enim vpetim koncem in drugim prostim koncem lahko začnemo s konstrukcijo diagramov Q in M ​​na prostem koncu, brez ugotavljanja reakcij v vgradnji. 1.2. Konstrukcija diagramov Q in M ​​z uporabo Beamovih enačb je razdeljena na odseke, znotraj katerih ostaneta funkciji za upogibni moment in strižno silo konstantni (nimata diskontinuitet). Meje odsekov so točke uporabe koncentriranih sil, parov sil in mest spremembe intenzivnosti porazdeljene obremenitve. Na vsakem odseku se vzame poljuben odsek na razdalji x od izhodišča koordinat in za ta odsek sestavijo enačbe za Q in M. Primer 1.1 Konstruirajte diagrame prečnice sile Q in upogibni momenti M za dani žarek (slika 1.4,a). Rešitev: 1. Določitev opornih reakcij. Sestavimo ravnotežne enačbe: iz katerih dobimo Reakcije nosilcev so pravilno določene. Žarek ima štiri dele, sl. 1.4 obremenitve: CA, AD, DB, BE. 2. Konstrukcija diagrama Q. Odsek CA. V preseku CA 1 narišemo poljuben presek 1-1 na razdalji x1 od levega konca nosilca. Definiramo Q kot algebraično vsoto vseh zunanjih sil, ki delujejo levo od odseka 1-1: znak minus je vzet, ker je sila, ki deluje levo od odseka, usmerjena navzdol. Izraz za Q ni odvisen od spremenljivke x1. Diagram Q v tem razdelku bo upodobljen kot ravna črta, vzporedna z osjo abscise. Oddelek AD. Na odseku narišemo poljuben odsek 2-2 na razdalji x2 od levega konca nosilca. Q2 definiramo kot algebraično vsoto vseh zunanjih sil, ki delujejo levo od odseka 2-2: 8 Vrednost Q je v odseku konstantna (ni odvisna od spremenljivke x2). Q graf na odseku je ravna črta, vzporedna z abscisno osjo. Plot DB. Na mestu narišemo poljuben odsek 3-3 na razdalji x3 od desnega konca nosilca. Definiramo Q3 kot algebraično vsoto vseh zunanjih sil, ki delujejo desno od odseka 3-3: Dobljeni izraz je enačba nagnjene ravne črte. Razdelek BE. Na mestu narišemo odsek 4-4 na razdalji x4 od desnega konca žarka. Definiramo Q kot algebraično vsoto vseh zunanjih sil, ki delujejo desno od odseka 4-4: 4 Tu je vzet znak plus, ker je rezultantna obremenitev desno od odseka 4-4 usmerjena navzdol. Na podlagi dobljenih vrednosti sestavimo Q diagrame (slika 1.4, b). 3. Konstrukcija diagrama M. Parcela m1. Upogibni moment v prerezu 1-1 definiramo kot algebraično vsoto momentov sil, ki delujejo levo od prereza 1-1. – enačba premice. Prerez A 3 Upogibni moment v prerezu 2-2 določimo kot algebraično vsoto momentov sil, ki delujejo levo od prereza 2-2. – enačba premice. Prerez DB 4 Upogibni moment v prerezu 3-3 določimo kot algebraično vsoto momentov sil, ki delujejo desno od prereza 3-3. – enačba kvadratne parabole. 9 Najdemo tri vrednosti na koncih odseka in v točki s koordinato xk, kjer Odsek BE 1 Določimo upogibni moment v odseku 4-4 kot algebraično vsoto momentov sil, ki delujejo desno od odseka 4-4. – enačba kvadratne parabole, najdemo tri vrednosti M4: Z uporabo dobljenih vrednosti sestavimo diagram M (slika 1.4, c). V odsekih CA in AD je diagram Q omejen z ravnimi črtami, vzporednimi z osjo abscise, v odsekih DB in BE pa z nagnjenimi ravnimi črtami. V prerezih C, A in B na diagramu Q so skoki v velikosti ustreznih sil, kar služi kot preverjanje pravilnosti grafa Q. V odsekih, kjer je Q  0, momenti naraščajo od leve proti desni. V območjih, kjer je Q  0, se momenti zmanjšajo. Pod zgoščenimi silami nastanejo pregibi v smeri delovanja sil. Pod koncentriranim momentom je skok v velikosti momenta. To kaže na pravilnost konstrukcije diagrama M. Primer 1.2 Konstruirajte diagrama Q in M ​​za nosilec na dveh nosilcih, obremenjenih s porazdeljeno obremenitvijo, katere intenzivnost se spreminja po linearnem zakonu (slika 1.5, a). Rešitev Določitev reakcij podpore. Rezultanta porazdeljene obremenitve je enaka površini trikotnika, ki je diagram obremenitve in deluje v težišču tega trikotnika. Sestavimo vsote momentov vseh sil glede na točki A in B: Sestavimo diagram Q. Narišimo poljuben prerez na razdalji x od levega nosilca. Ordinata diagrama obremenitve, ki ustreza odseku, se določi iz podobnosti trikotnikov. Rezultanta tistega dela obremenitve, ki se nahaja levo od odseka. Prečna sila v odseku je enaka. Prečna sila se spreminja po zakonu kvadratne parabole Če enačimo enačbo prečne sile na nič, najdemo absciso odseka, v katerem gre diagram Q skozi nič: Q graf je prikazan na sl. 1.5, b. Upogibni moment v poljubnem odseku je enak Upogibni moment se spreminja po zakonu kubične parabole: Upogibni moment ima največjo vrednost v odseku, kjer je 0, to je na diagramu M, prikazanem na sl. 1,5, c. 1.3. Izdelava diagramov Q in M ​​iz značilnih odsekov (točk) Z uporabo diferencialnih odvisnosti med M, Q, q in sklepi, ki izhajajo iz njih, je priporočljivo sestaviti diagrame Q in M ​​iz značilnih odsekov (brez sestavljanja enačb). S to metodo se vrednosti Q in M ​​izračunajo v značilnih odsekih. Karakteristični odseki so mejni odseki odsekov, pa tudi odseki, kjer ima dani faktor notranje sile ekstremno vrednost. Znotraj meja med značilnimi odseki je oris 12 diagrama vzpostavljen na podlagi diferencialnih odvisnosti med M, Q, q in iz njih izhajajočih zaključkov. Primer 1.3 Konstruirajte diagrama Q in M ​​za žarek, prikazan na sl. 1.6, a. riž. 1.6. Rešitev: Q in M ​​diagrama začnemo sestavljati od prostega konca žarka, pri čemer reakcij v vgradnji ni treba ugotavljati. Nosilec ima tri obremenitvene odseke: AB, BC, CD. V odsekih AB in BC ni porazdeljene obremenitve. Strižne sile so konstantne. Diagram Q je omejen na ravne črte, vzporedne z osjo x. Upogibni momenti se spreminjajo linearno. Diagram M je omejen z ravnimi črtami, nagnjenimi na abscisno os. Na odseku CD je enakomerno porazdeljena obremenitev. Prečne sile se spreminjajo po linearnem zakonu, upogibni momenti pa po zakonu kvadratne parabole s konveksnostjo v smeri porazdeljene obremenitve. Na meji odsekov AB in BC se prečna sila sunkovito spremeni. Na meji odsekov BC in CD se upogibni moment nenadoma spremeni. 1. Konstrukcija diagrama Q. Izračunamo vrednosti prečnih sil Q v mejnih odsekih odsekov: Na podlagi rezultatov izračuna sestavimo diagram Q za žarek (slika 1, b). Iz diagrama Q sledi, da je prečna sila na odseku CD enaka nič v odseku, ki se nahaja na razdalji qa a q od začetka tega odseka. V tem odseku ima upogibni moment največjo vrednost. 2. Izdelava diagrama M. Izračunamo vrednosti upogibnih momentov v mejnih odsekih odsekov: Pri največjem momentu v odseku Na podlagi rezultatov izračuna sestavimo diagram M (sl. 5.6, c). Primer 1.4 Z danim diagramom upogibnih momentov (sl. 1.7, a) za žarek (sl. 1.7, b) določite delujoče obremenitve in sestavite diagram Q. Krog označuje vrh kvadratne parabole. Rešitev: Določimo obremenitve, ki delujejo na nosilec. Odsek AC je obremenjen z enakomerno porazdeljeno obremenitvijo, saj je diagram M v tem odseku kvadratna parabola. V referenčnem odseku B se na žarek nanaša koncentrirani moment, ki deluje v smeri urinega kazalca, saj imamo v diagramu M skok navzgor za velikost momenta. V SV odseku greda ni obremenjena, saj je M diagram v tem odseku omejen z nagnjeno premico. Reakcija nosilca B je določena iz pogoja, da je upogibni moment v odseku C enak nič, tj. Za določitev intenzivnosti porazdeljene obremenitve ustvarimo izraz za upogibni moment v odseku A kot vsoto momentov sile na desni in jo izenačimo z ničlo Sedaj določimo reakcijo nosilca A. Da bi to naredili, bomo sestavili izraz za upogibne momente v prerezu kot vsoto momentov sil na levi strani. Diagram konstrukcije nosilca z obremenitvijo je prikazan na sl. 1.7, c. Začenši z levega konca žarka, izračunamo vrednosti prečnih sil v mejnih odsekih odsekov: Diagram Q je prikazan na sl. 1.7, d. Obravnavani problem je mogoče rešiti z izdelavo funkcionalnih odvisnosti za M, Q v vsakem odseku. Izberimo izhodišče koordinat na levem koncu žarka. V odseku AC je diagram M izražen s kvadratno parabolo, katere enačba ima obliko. Konstante a, b, c dobimo iz pogoja, da parabola poteka skozi tri točke z znanimi koordinatami: Zamenjava koordinat točk v enačbo parabole dobimo: Izraz za upogibni moment dobimo z diferenciranjem funkcije M1 dobimo odvisnost za prečno silo Po diferenciranju funkcije Q dobimo izraz za intenzivnost porazdeljene obremenitve. V odseku NE je izraz za upogibni moment predstavljen v obliki linearne funkcije. Za določitev konstant a in b uporabimo pogoje, da ta premica poteka skozi dve točki, katerih koordinate so znane dobimo dve enačbi: ,b iz katere dobimo 20. Enačba za upogibni moment v odseku NE bo po dvojni diferenciaciji M2, bomo z najdenimi vrednostmi M in Q sestavili diagrame upogibni momenti in strižne sile za nosilec. Poleg porazdeljene obremenitve na nosilec delujejo zgoščene sile v treh odsekih, kjer so skoki na diagramu Q in zgoščeni momenti v odseku, kjer je udarec na diagramu M. Primer 1.5 Za žarek (slika 1.8, a) določite racionalni položaj tečaja C, pri katerem je največji upogibni moment v razponu enak upogibnemu momentu v vgradnji (v absolutni vrednosti). Sestavite diagrama Q in M. Rešitev Določitev reakcij podpore. Kljub dejstvu, da je skupno število nosilnih členov štiri, je nosilec statično determiniran. Upogibni moment v tečaju C je enak nič, kar nam omogoča, da sestavimo dodatno enačbo: vsota momentov okoli tečaja vseh zunanjih sil, ki delujejo na eni strani tega tečaja, je enaka nič. Sestavimo vsoto momentov vseh sil desno od tečaja C. Diagram Q za nosilec je omejen z nagnjeno ravnino, saj je q = const. Določimo vrednosti prečnih sil v mejnih odsekih nosilca: Absciso xK odseka, kjer je Q = 0, določimo iz enačbe, iz katere je diagram M za nosilec omejen s kvadratno parabolo. Izraza za upogibne momente v prerezih, kjer je Q = 0, in v vložku zapišemo takole: Iz pogoja enakosti momentov dobimo kvadratno enačbo za želeni parameter x: Realna vrednost x2x 1.029 m. Določimo številčne vrednosti prečnih sil in upogibnih momentov v značilnih odsekih žarka. Slika 1.8, b prikazuje diagram Q, na sl. 1.8, c - diagram M. Obravnavani problem je mogoče rešiti z razdelitvijo zgibnega nosilca na njegove sestavne elemente, kot je prikazano na sl. 1.8, d. Na začetku so določene reakcije nosilcev VC in VB. Diagrami Q in M ​​so izdelani za viseči nosilec SV glede na delovanje obremenitve, ki se nanj nanaša. Nato se premaknejo na glavni nosilec AC in ga obremenijo z dodatno silo VC, ki je sila pritiska nosilca CB na nosilec AC. Po tem se zgradita diagrama Q in M ​​za žarek AC. 1.4. Izračuni trdnosti za direktni upogib nosilcev Izračuni trdnosti na podlagi normalnih in strižnih napetosti. Ko se žarek upogne neposredno v svojih prerezih, nastanejo normalne in tangencialne napetosti (slika 1.9). 18 sl. 1.9 Normalne napetosti so povezane z upogibnim momentom, tangencialne napetosti so povezane s strižno silo. Pri ravnem čistem upogibu so strižne napetosti nič. Normalne napetosti na poljubni točki prečnega prereza nosilca so določene s formulo (1.4) kjer je M upogibni moment v danem odseku; Iz – vztrajnostni moment preseka glede na nevtralno os z; y je razdalja od točke, kjer je določena normalna napetost, do nevtralne osi z. Normalne napetosti vzdolž višine odseka se spreminjajo po linearnem zakonu in dosežejo največjo vrednost v točkah, ki so najbolj oddaljene od nevtralne osi. Če je odsek simetričen glede na nevtralno os (sl. 1.11), potem sl. 1.11 so največje natezne in tlačne napetosti enake in so določene s formulo,  je osni moment upora odseka med upogibanjem. Za pravokotni odsek s širino b in višino h: (1.7) Za krožni odsek s premerom d: (1.8) Za obročasti odsek   – notranji oziroma zunanji premer obroča. Za nosilce iz plastičnih materialov so najbolj racionalne simetrične oblike 20 presekov (I-žarek, škatlasti, obročasti). Za nosilce iz krhkih materialov, ki se ne upirajo enako napetosti in stiskanju, so racionalni odseki, ki so asimetrični glede na nevtralno os z (T-žarek, U-oblika, asimetrični I-žarek). Za nosilce stalnega prereza iz plastičnih materialov s simetričnimi oblikami prereza je pogoj trdnosti zapisan takole: (1.10) kjer je Mmax največji upogibni moment v modulu; – dovoljena napetost za material. Za nosilce stalnega prereza iz plastičnih mas z nesimetričnimi oblikami preseka se pogoj trdnosti zapiše v obliki: (1. 11) Za nosilce iz krhkih materialov z odseki, ki so asimetrični glede na nevtralno os, če je diagram M nedvoumen (slika 1.12), je treba zapisati dva pogoja trdnosti - razdaljo od nevtralne osi do najbolj oddaljene točke raztegnjenega oziroma stisnjenega območja nevarnega odseka; P – dovoljene napetosti za napetost oziroma stiskanje. Slika 1.12. 21 Če ima diagram upogibnih momentov odseke različnih znakov (sl. 1.13), potem je poleg preverjanja odseka 1-1, kjer deluje Mmax, potrebno izračunati največje natezne napetosti za odsek 2-2 (z najvišjo trenutek nasprotnega predznaka). riž. 1.13 Skupaj z glavnim izračunom z uporabo normalnih napetosti je v številnih primerih potrebno preveriti trdnost žarka s tangencialnimi napetostmi. Tangencialne napetosti v nosilcih se izračunajo po formuli D.I. Zhuravsky (1.13), kjer je Q prečna sila v prerezu obravnavanega nosilca; Szотс - statični moment glede na nevtralno os območja dela preseka, ki se nahaja na eni strani ravne črte, narisane skozi dano točko in vzporedno z osjo z; b – širina preseka na ravni obravnavane točke; Iz je vztrajnostni moment celotnega odseka glede na nevtralno os z. V mnogih primerih se največje strižne napetosti pojavijo na ravni nevtralne plasti nosilca (pravokotnik, I-nosilec, krog). V takih primerih se trdnostni pogoj za tangencialne napetosti zapiše v obliki, (1.14) kjer je Qmax največja prečna sila v absolutni vrednosti; – dopustna strižna napetost materiala. Za pravokotni odsek žarka ima pogoj trdnosti obliko (1.15) A je površina prečnega prereza žarka. Za krožni odsek je trdnostni pogoj predstavljen v obliki (1.16) Za I-prerez je trdnostni pogoj zapisan takole: (1.17) kjer je Szo,тmсax statični moment polpreseka glede na nevtralno os; d – debelina stene I-nosilca. Običajno se dimenzije prečnega prereza nosilca določijo iz stanja trdnosti pri normalnih napetostih. Preverjanje trdnosti nosilcev s strižno napetostjo je obvezno za kratke nosilce in nosilce katere koli dolžine, če so v bližini nosilcev koncentrirane sile velikega obsega, pa tudi za lesene, kovičene in varjene nosilce. Primer 1.6 Preverite trdnost nosilca škatlastega prereza (slika 1.14) z uporabo normalnih in strižnih napetosti, če je MPa. Konstruirajte diagrame v nevarnem delu žarka. riž. 1.14 Rešitev 23 1. Izdelava diagramov Q in M ​​z uporabo karakterističnih odsekov. Če upoštevamo levo stran nosilca, dobimo Diagram prečnih sil je prikazan na sl. 1.14, c. Diagram upogibnih momentov je prikazan na sl. 5.14, g 2. Geometrijske značilnosti prereza 3. Najvišje normalne napetosti v prerezu C, kjer deluje Mmax (modulo): MPa. Največje normalne napetosti v nosilcu so skoraj enake dovoljenim. 4. Največje tangencialne napetosti v prerezu C (ali A), kjer deluje max Q (modulo): Tukaj je statični moment površine polprereza glede na nevtralno os; b2 cm – širina preseka v višini nevtralne osi. 5. Tangencialne napetosti v točki (v steni) v prerezu C: sl. 1.15 Tukaj je Szomc 834,5 108 cm3 statični moment površine dela odseka, ki se nahaja nad črto, ki poteka skozi točko K1; b2 cm – debelina stene na nivoju točke K1. Diagrama  in  za odsek C žarka sta prikazana na sl. 1.15. Primer 1.7 Za žarek, prikazan na sl. 1.16, a, zahtevano: 1. Konstruirajte diagrame prečnih sil in upogibnih momentov vzdolž značilnih odsekov (točk). 2. Določite dimenzije prečnega prereza v obliki kroga, pravokotnika in I-žarka iz pogoja trdnosti pri normalnih napetostih, primerjajte površine prečnega prereza. 3. Preverite izbrane dimenzije odsekov nosilca glede na tangencialno napetost. Podano: Rešitev: 1. Določite reakcije nosilcev nosilca. Preverite: 2. Konstrukcija diagramov Q in M. Vrednosti prečnih sil v karakterističnih odsekih nosilca 25 Sl. 1.16 V prerezih CA in AD je intenzivnost obremenitve q = const. Posledično je na teh območjih diagram Q omejen na ravne črte, nagnjene na os. V odseku DB je intenzivnost porazdeljene obremenitve q = 0, zato je v tem odseku diagram Q omejen na ravno črto, vzporedno z osjo x. Q diagram za žarek je prikazan na sl. 1.16, b. Vrednosti upogibnih momentov v značilnih odsekih nosilca: V drugem odseku določimo absciso x2 odseka, v katerem je Q = 0: Največji moment v drugem odseku Diagram M za nosilec je prikazan na sl. 1.16, c. 2. Ustvarimo pogoj trdnosti, ki temelji na normalnih napetostih, iz katerih določimo zahtevani osni moment upora odseka iz izraza, določenega z zahtevanim premerom d žarka krožnega odseka. Za žarek pravokotnega odseka določite potrebno višino prereza. Z uporabo tabel GOST 8239-89 najdemo najbližjo višjo vrednost aksialnega momenta upora 597 cm3, kar ustreza I-žarku št. 33 z značilnostmi: A z 9840 cm4. Preverjanje tolerance: (podobremenitev za 1% od dovoljenih 5%) najbližji I-nosilec št. 30 (W 2 cm3) povzroči znatno preobremenitev (več kot 5%). Končno sprejmemo I-žarek št. 33. Primerjamo površine okroglega in pravokotnega odseka z najmanjšo površino A I-žarka: Od treh obravnavanih odsekov je najbolj ekonomičen odsek I-žarka. 3. Izračunamo najvišje normalne napetosti v nevarnem odseku 27 I-žarka (sl. 1.17, a): Normalne napetosti v steni blizu prirobnice odseka I-žarka Diagram normalnih napetosti v nevarnem odseku žarek je prikazan na sl. 1.17, b. 5. Določite največje strižne napetosti za izbrane odseke nosilca. a) pravokotni prerez nosilca: b) okrogel prerez nosilca: c) prerez I-nosilca: Tangencialne napetosti v steni blizu prirobnice I-nosilca v nevarnem odseku A (desno) (pri točki 2): diagram tangencialnih napetosti v nevarnih odsekih I-nosilca je prikazan na sl. 1.17, c. Največje tangencialne napetosti v nosilcu ne presegajo dovoljenih napetosti. Primer 1.8 Določite dovoljeno obremenitev nosilca (slika 1.18, a), če je 60 MPa, so podane dimenzije preseka (slika 1.19, a). Izdelajte diagram normalnih napetosti v nevarnem delu nosilca pri dovoljeni obremenitvi. Slika 1.18 1. Določanje reakcij nosilcev nosilca. Zaradi simetričnosti sistema 2. Izdelava diagramov Q in M ​​iz karakterističnih prerezov. Prečne sile v značilnih odsekih nosilca: Diagram Q za nosilec je prikazan na sl. 5.18, b. Upogibni momenti v značilnih odsekih nosilca Za drugo polovico nosilca so ordinate M vzdolž simetrijskih osi. Diagram M za žarek je prikazan na sl. 1.18, b. 3. Geometrijske značilnosti odseka (slika 1.19). Figuro razdelimo na dva preprosta elementa: I-žarek - 1 in pravokotnik - 2. Sl. 1.19 Glede na sortiment za I-nosilec št. 20 imamo Za pravokotnik: Statični moment površine preseka glede na os z1 Razdalja od osi z1 do težišča preseka Vztrajnostni moment relativnega preseka na glavno središčno os z celotnega odseka v skladu s formulami za prehod na vzporedne osi 4. Pogoj trdnosti za normalne napetosti za nevarno točko "a" (sl. 1.19) v nevarnem odseku I (sl. 1.18): Po zamenjavi numerični podatki 5. Pri dovoljeni obremenitvi v nevarnem odseku bodo normalne napetosti v točkah "a" in "b" enake: Diagram normalnih napetosti za nevarni odsek 1-1 je prikazan na sl. 1.19, b.