Kõige kuulsam rohkem kui nelja nurgaga kuju on tavaline kuusnurk. Geomeetrias kasutatakse seda sageli probleemide lahendamisel. Ja elus just sellised kärjed lõikamisel välja näevad.
Kuidas see erineb valest?
Esiteks on kuusnurk 6 tipuga kujund. Teiseks võib see olla kumer või nõgus. Esimene erineb selle poolest, et neli tippu asuvad läbi ülejäänud kahe sirge ühel küljel.
Kolmandaks, korrapärast kuusnurka iseloomustab asjaolu, et selle kõik küljed on võrdsed. Pealegi on igal joonise nurgal sama tähendus. Kõigi selle nurkade summa määramiseks peate kasutama valemit: 180º * (n - 2). Siin on n joonise tippude arv, see tähendab 6. Lihtne arvutus annab väärtuseks 720º. See tähendab, et iga nurk on 120 kraadi.
Igapäevatoimingutes leidub korrapärast kuusnurka lumehelves ja pähklis. Keemikud näevad seda isegi benseeni molekulis.
Milliseid omadusi pead probleemide lahendamisel teadma?
Eespool kirjeldatule tuleks lisada:
- läbi keskpunkti tõmmatud kujundi diagonaalid jagavad selle kuueks kolmnurgaks, mis on võrdkülgsed;
- korrapärase kuusnurga külje väärtus langeb kokku selle ümber oleva ringi raadiusega;
- Sellist joonist kasutades on võimalik tasapinda täita ning nende vahele ei jää lünki ega kattumisi.
Kasutusele võetud nimetused
Traditsiooniliselt tähistatakse tavalise geomeetrilise kujundi külge ladina tähega "a". Ülesannete lahendamiseks on vaja ka pindala ja perimeetrit, need on vastavalt S ja P. Ringi saab kirjutada korrapärasesse kuusnurka või kirjeldada selle ümber. Seejärel sisestatakse nende raadiuste väärtused. Neid tähistatakse vastavalt tähtedega r ja R.
Mõned valemid sisaldavad sisenurka, poolperimeetrit ja apoteemi (mis on hulknurga keskpunktist mis tahes külje keskkohaga risti). Nende jaoks kasutatakse järgmisi tähti: α, р, m.
Valemid, mis kirjeldavad figuuri
Sissekirjutatud ringi raadiuse arvutamiseks vajate järgmist: r = (a * √3) / 2, kus r = m. See tähendab, et sama valem on apoteemi jaoks.
Kuna kuusnurga ümbermõõt on kõigi külgede summa, määratakse see järgmiselt: P = 6 * a. Võttes arvesse asjaolu, et külg on võrdne sisse kirjutatud ringi raadiusega, on ümbermõõdu jaoks korrapärase kuusnurga jaoks järgmine valem: P = 6 * R. Ringjoone raadiuse jaoks antud valem on tuletatakse seos a ja r vahel. Siis saab valem järgmise kuju: P = 4 r * √3.
Tavalise kuusnurga pindala jaoks võib olla kasulik järgmine: S = p * r = (a 2 * 3 √3) / 2.
Ülesanded
Nr 1. Seisukord. Seal on tavaline kuusnurkne prisma, mille iga serv on 4 cm, millesse on sisse kirjutatud silinder, mille maht tuleb leida.
Lahendus. Silindri maht on defineeritud kui aluse pindala ja kõrguse korrutis. Viimane langeb kokku prisma servaga. Ja see on võrdne tavalise kuusnurga küljega. See tähendab, et silindri kõrgus on samuti 4 cm.
Selle aluse pindala väljaselgitamiseks peate arvutama kuusnurka kirjutatud ringi raadiuse. Selle valem on toodud ülal. See tähendab, et r = 2√3 (cm). Siis ringi pindala: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (cm 2).
Vastus. V = 150,72 cm3.
Nr 2. Seisukord. Arvutage korrapärasesse kuusnurka kirjutatud ringi raadius. On teada, et selle külg on √3 cm. Millega võrdub selle ümbermõõt?
Lahendus. See probleem nõuab kahe järgmise valemi kasutamist. Pealegi tuleb neid rakendada ilma neid isegi muutmata, lihtsalt asendage külje väärtus ja arvutage.
Seega on sisse kirjutatud ringi raadius võrdne 1,5 cm Perimeetri jaoks osutub õigeks järgmine väärtus: 6√3 cm.
Vastus. r = 1,5 cm, P = 6√3 cm.
Nr 3. Seisukord. Piiratud ringi raadius on 6 cm. Mis väärtus on sel juhul tavalise kuusnurga küljel?
Lahendus. Kuusnurka kantud ringi raadiuse valemist saate hõlpsalt selle, mille järgi peate külje arvutama. On selge, et raadius korrutatakse kahega ja jagatakse kolme juurega. Nimetajas on vaja vabaneda irratsionaalsusest. Seetõttu on toimingute tulemus järgmine: (12 √3) / (√3 * √3), see tähendab 4√3.
Vastus. a = 4√3 cm.
Kas sa tead, milline näeb välja tavaline kuusnurk?
Seda küsimust ei küsitud juhuslikult. Enamik 11. klassi õpilasi ei tea sellele vastust.
Tavaline kuusnurk on selline, mille kõik küljed on võrdsed ja kõik nurgad on samuti võrdsed..
Raudmutter. Lumehelves. Kärgstruktuuri rakk, milles elavad mesilased. Benseeni molekul. Mis on neil objektidel ühist? - Asjaolu, et neil kõigil on korrapärane kuusnurkne kuju.
Paljud koolilapsed satuvad segadusse, kui nad näevad korrapärase kuusnurgaga seotud probleeme ja usuvad, et nende lahendamiseks on vaja spetsiaalseid valemeid. On see nii?
Joonistame korrapärase kuusnurga diagonaalid. Saime kuus võrdkülgset kolmnurka. 
Teame, et korrapärase kolmnurga pindala on: .
Siis on tavalise kuusnurga pindala kuus korda suurem.
Kus on tavalise kuusnurga külg.
Pange tähele, et tavalises kuusnurgas on kaugus selle keskpunktist ükskõik millise tipuni sama ja võrdne tavalise kuusnurga küljega.
See tähendab, et korrapärase kuusnurga ümber piiratud ringi raadius on võrdne selle küljega.
Korrapärasesse kuusnurka kirjutatud ringi raadiust pole raske leida.
See on võrdne.
Nüüd saate hõlpsasti lahendada kõik USE probleemid, mis hõlmavad tavalist kuusnurka.
Leidke korrapärasesse kuusnurka kantud ringi raadius, mille külg on .
Sellise ringi raadius on võrdne .
Vastus: .
Mis on korrapärase kuusnurga külg, mis on kirjutatud ringi, mille raadius on 6?
Teame, et korrapärase kuusnurga külg on võrdne selle ümber oleva ringi raadiusega.
Kas sa tead, milline näeb välja tavaline kuusnurk?
Seda küsimust ei küsitud juhuslikult. Enamik 11. klassi õpilasi ei tea sellele vastust.
Tavaline kuusnurk on selline, mille kõik küljed on võrdsed ja kõik nurgad on samuti võrdsed..
Raudmutter. Lumehelves. Kärgstruktuuri rakk, milles elavad mesilased. Benseeni molekul. Mis on neil objektidel ühist? - Asjaolu, et neil kõigil on korrapärane kuusnurkne kuju.
Paljud koolilapsed satuvad segadusse, kui nad näevad korrapärase kuusnurgaga seotud probleeme ja usuvad, et nende lahendamiseks on vaja spetsiaalseid valemeid. On see nii?
Joonistame korrapärase kuusnurga diagonaalid. Saime kuus võrdkülgset kolmnurka.
Teame, et korrapärase kolmnurga pindala on: .
Siis on tavalise kuusnurga pindala kuus korda suurem.
Kus on tavalise kuusnurga külg.
Pange tähele, et tavalises kuusnurgas on kaugus selle keskpunktist ükskõik millise tipuni sama ja võrdne tavalise kuusnurga küljega.
See tähendab, et korrapärase kuusnurga ümber piiratud ringi raadius on võrdne selle küljega.
Korrapärasesse kuusnurka kirjutatud ringi raadiust pole raske leida.
See on võrdne.
Nüüd saate hõlpsasti lahendada kõik USE probleemid, mis hõlmavad tavalist kuusnurka.
Leidke korrapärasesse kuusnurka kantud ringi raadius, mille külg on .
Sellise ringi raadius on võrdne .
Vastus: .
Mis on korrapärase kuusnurga külg, mis on kirjutatud ringi, mille raadius on 6?
Teame, et korrapärase kuusnurga külg on võrdne selle ümber oleva ringi raadiusega.
Ringi sisse kirjutatud korrapärase kuusnurga ehitus. Kuusnurga ehitus põhineb asjaolul, et selle külg on võrdne piiritletud ringi raadiusega. Seetõttu piisab selle konstrueerimiseks jagada ring kuueks võrdseks osaks ja ühendada leitud punktid omavahel (joon. 60, a).
Tavalise kuusnurga saab ehitada sirge serva ja 30X60° ruudu abil. Selle konstruktsiooni teostamiseks võtame nurkade 1 ja 4 poolitajaks ringi horisontaalse läbimõõdu (joonis 60, b), konstrueerime küljed 1 -6, 4-3, 4-5 ja 7-2, mille järel tõmbame küljed 5-6 ja 3-2.
Ringjoone sisse kirjutatud võrdkülgse kolmnurga konstrueerimine. Sellise kolmnurga tippe saab konstrueerida kasutades kompassi ja ruutu, mille nurgad on 30 ja 60° või ainult ühe kompassi abil.
Vaatleme kahte võimalust ringi sisse kirjutatud võrdkülgse kolmnurga konstrueerimiseks.
Esimene viis(joonis 61,a) põhineb asjaolul, et kolmnurga 7, 2, 3 kõik kolm nurka sisaldavad 60° ja läbi punkti 7 tõmmatud vertikaaljoon on nii nurga 1 kõrgus kui ka poolitaja. on 0-1- 2 võrdub 30°, siis külje leidmiseks
1-2, piisab, kui konstrueerida punktist 1 ja küljest 0-1 nurk 30°. Selleks paigaldage risttala ja ruut, nagu joonisel näidatud, tõmmake joon 1-2, mis on soovitud kolmnurga üks külgedest. Külje 2-3 ehitamiseks seadke risttala katkendjoontega näidatud asendisse ja tõmmake läbi punkti 2 sirgjoon, mis määrab kolmnurga kolmanda tipu.
Teine viis põhineb asjaolul, et kui ehitada ringikujuline korrapärane kuusnurk ja seejärel ühendada selle tipud läbi ühe, saate võrdkülgse kolmnurga.
Kolmnurga konstrueerimiseks (joonis 61, b) märgi läbimõõdule tipp-punkt 1 ja tõmba diameetriline joon 1-4. Järgmisena kirjeldame punktist 4, mille raadius on võrdne D/2-ga, kaare, kuni see lõikub ringiga punktides 3 ja 2. Saadud punktid on soovitud kolmnurga kaks ülejäänud tippu.
Ringi sisse kirjutatud ruudu konstrueerimine. Seda konstruktsiooni saab teha ruudu ja kompassi abil.
Esimene meetod põhineb asjaolul, et ruudu diagonaalid lõikuvad piiritletud ringi keskpunktis ja on selle telgede suhtes 45° nurga all. Sellest lähtuvalt paigaldame risttala ja ruudu 45° nurga all, nagu on näidatud joonisel fig. 62, a ja märgi punktid 1 ja 3. Järgmiseks joonistame nende punktide kaudu risttala abil ruudu horisontaalsed küljed 4-1 ja 3-2. Seejärel joonistame sirge serva abil ruudu vertikaalsed küljed 1-2 ja 4-3 piki ruudu jalga.
Teine meetod põhineb asjaolul, et ruudu tipud poolitavad läbimõõdu otste vahele jääva ringi kaared (joon. 62, b). Märgime punktid A, B ja C kahe vastastikku risti asetseva diameetri otstesse ning nendest raadiusega y kirjeldame kaare, kuni need ristuvad.
Järgmisena joonistame läbi kaare ristumispunktide abisirged, mis on joonisel tähistatud pidevate joontega. Nende ristumispunktid ringiga määravad ära tipud 1 ja 3; 4 ja 2. Ühendame sel viisil saadud soovitud ruudu tipud üksteisega järjestikku.
Ringi sisse kirjutatud korrapärase viisnurga ehitus.
Korrapärase viisnurga sobitamiseks ringiks (joonis 63) teeme järgmised konstruktsioonid.
Märgime ringile punkti 1 ja võtame selle üheks viisnurga tipuks. Jagame segmendi AO pooleks. Selleks kirjeldame kaare punktist A raadiusega AO, kuni see lõikub ringiga punktides M ja B. Ühendades need punktid sirgjoonega, saame punkti K, mille seejärel ühendame punktiga 1. raadius, mis on võrdne lõiguga A7, kirjeldame kaare punktist K, kuni see lõikub punktis H diametraaljoonega AO. Ühendades punkti 1 punktiga H, saame viisnurga külje. Seejärel, kasutades lõiguga 1H võrduvat kompassilahendust, kirjeldades kaare tipust 1 kuni ringjoone lõikepunktini, leiame tipud 2 ja 5. Olles teinud sama kompassilahendusega tippudest 2 ja 5 sälgud, saame ülejäänud tipud 3 ja 4. Leitud punktid ühendame üksteisega järjestikku.
Korrapärase viisnurga konstrueerimine piki etteantud külge.
Korrapärase viisnurga konstrueerimiseks piki etteantud külge (joonis 64) jagame lõigu AB kuueks võrdseks osaks. Punktidest A ja B raadiusega AB kirjeldame kaare, mille lõikepunktist saab punkti K. Läbi selle punkti ja jaotuse 3 sirgel AB tõmbame vertikaalse sirge.
Saame viisnurga punkti 1 tipu. Seejärel kirjeldame raadiusega, mis on võrdne AB-ga, punktist 1 kaare, kuni see lõikub punktidest A ja B eelnevalt tõmmatud kaaredega. Kaarte lõikepunktid määravad viisnurga tipud 2 ja 5. Leitud tipud ühendame seeriad omavahel.
Ringi sisse kirjutatud korrapärase seitsenurga ehitus.
Olgu antud ring läbimõõduga D; sellesse tuleb mahutada tavaline seitsenurk (joonis 65). Jagage ringi vertikaalne läbimõõt seitsmeks võrdseks osaks. Punktist 7, mille raadius on võrdne ringi D läbimõõduga, kirjeldame kaare, kuni see lõikub horisontaalse läbimõõdu jätkuga punktis F. Punkti F nimetame hulknurga pooluseks. Võttes seitsenurga üheks tipuks punkti VII, tõmbame poolusest F kiirid läbi vertikaalse läbimõõdu ühtlaste jaotuste, mille ristumiskohas ringjoonega määratakse seitsenurga tipud VI, V ja IV. Punktidest IV, V ja VI tippude / - // - /// saamiseks tõmmake horisontaaljooni, kuni need ristuvad ringiga. Leitud tipud ühendame üksteisega järjestikku. Seitsmenurga saab konstrueerida, tõmmates kiiri F-poolusest ja läbi vertikaalse läbimõõdu paaritu jaotuse.
Ülaltoodud meetod sobib mistahes arvu külgedega korrapäraste hulknurkade konstrueerimiseks.
Ringi jagamist suvaliseks arvuks võrdseteks osadeks saab teha ka tabelis olevate andmete abil. 2, mis annab koefitsiendid, mis võimaldavad määrata korrapäraste sissekirjutatud hulknurkade külgede mõõtmeid.
Kooli õppekavas on polügoonide teemat käsitletud, kuid sellele ei pöörata piisavalt tähelepanu. Vahepeal on see huvitav ja see kehtib eriti tavalise kuusnurga või kuusnurga kohta - paljudel loodusobjektidel on ju selline kuju. Nende hulka kuuluvad kärjed ja palju muud. See vorm töötab praktikas väga hästi.
Definitsioon ja ehitus
Tavaline kuusnurk on tasapinnaline kujund, millel on kuus võrdse pikkusega külge ja sama arv võrdseid nurki.
Kui meenutada hulknurga nurkade summa valemit
selgub, et sellel joonisel on see 720°. Noh, kuna kõik joonise nurgad on võrdsed, pole raske arvutada, et igaüks neist võrdub 120 °.
Kuusnurga joonistamine on väga lihtne; kõik, mida vajate, on kompass ja joonlaud.
Samm-sammulised juhised näevad välja järgmised:
Soovi korral saate ilma jooneta hakkama, joonistades viis võrdse raadiusega ringi.
Nii saadud kujund on tavaline kuusnurk ja seda saab allpool tõestada.
Omadused on lihtsad ja huvitavad
Tavalise kuusnurga omaduste mõistmiseks on mõttekas jagada see kuueks kolmnurgaks:
See aitab tulevikus selgemalt kuvada selle omadusi, millest peamised on:
- piiritletud ringi läbimõõt;
- sisse kirjutatud ringi läbimõõt;
- ruut;
- ümbermõõt.
Piiratud ring ja konstrueeritavus
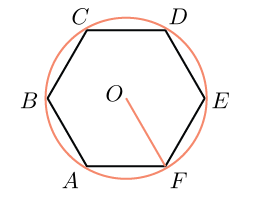
Ringi saab kirjeldada ümber kuusnurga ja ainult ühte. Kuna see arv on korrapärane, saate seda teha üsna lihtsalt: joonistage seespool kahest kõrvuti asetsevast nurgast poolitaja. Need lõikuvad punktis O ja moodustavad koos nendevahelise küljega kolmnurga.
Nurgad kuusnurga külje ja poolitajate vahel on 60°, seega võib kindlalt väita, et kolmnurk, näiteks AOB, on võrdhaarne. Ja kuna kolmas nurk on samuti 60°, on see ka võrdkülgne. Sellest järeldub, et segmendid OA ja OB on võrdsed, mis tähendab, et need võivad olla ringi raadius.
Pärast seda saate liikuda järgmisele küljele ja joonistada ka poolitaja punktis C olevast nurgast. Saate teise võrdkülgse kolmnurga ja külg AB on mõlema jaoks ühine ja OS on järgmine raadius, mida läbib sama ring. Selliseid kolmnurki on kokku kuus ja neil on ühine tipp punktis O. Selgub, et ringjoont on võimalik kirjeldada ja sellest on ainult üks ja selle raadius on võrdne ringi küljega. kuusnurk:
Seetõttu on võimalik seda kujundit konstrueerida kompassi ja joonlaua abil.
Noh, selle ringi pindala on standardne:
Sisse kirjutatud ring
Ümberringi keskpunkt langeb kokku kirjutatud ringi keskpunktiga. Selle kontrollimiseks võite tõmmata punktist O kuusnurga külgedele risti. Need on kuusnurga moodustavate kolmnurkade kõrgused. Ja võrdhaarse kolmnurga puhul on kõrgus selle külje mediaan, millele see toetub. Seega pole see kõrgus midagi muud kui risti poolitaja, mis on sisse kirjutatud ringi raadius.
Võrdkülgse kolmnurga kõrgus arvutatakse lihtsalt:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
Ja kuna R=a ja r=h, siis selgub, et
r=R(√3)/2.
Seega läbib ringjoon korrapärase kuusnurga külgede keskpunkte.
Selle pindala saab olema:
S=3πa²/4,
ehk kolmveerand kirjeldatust.
Perimeeter ja pindala
Perimeetriga on kõik selge, see on külgede pikkuste summa:
P=6a, või P=6R
Kuid pindala on võrdne kõigi kuue kolmnurga summaga, milleks saab kuusnurga jagada. Kuna kolmnurga pindala arvutatakse poolena aluse ja kõrguse korrutisest, siis:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 või
S=3R²(√3)/2
Need, kes soovivad arvutada selle pindala läbi kirjutatud ringi raadiuse, saavad teha järgmist:
S=3(2r/√3)²(√3)/2=r²(2√3)
Meelelahutuslikud konstruktsioonid
Kolmnurga saab mahutada kuusnurka, mille küljed ühendavad tipud läbi ühe:
Neid on kokku kaks ja nende kattumine annab Taaveti tähe. Kõik need kolmnurgad on võrdkülgsed. Seda pole raske kontrollida. Kui vaadata vahelduvvoolu külge, siis see kuulub korraga kahte kolmnurka – BAC ja AEC. Kui esimeses neist AB = BC ja nende vaheline nurk on 120°, siis on kõik ülejäänud 30°. Sellest saame teha loogilisi järeldusi:
- Kõrgus ABC tipust B võrdub poole kuusnurga küljega, kuna sin30°=1/2. Neile, kes soovivad seda kontrollida, võib soovitada ümber arvutada, kasutades Pythagorase teoreemi, see sobib siia suurepäraselt.
- Külg AC võrdub sissekirjutatud ringi kahe raadiusega, mis arvutatakse uuesti sama teoreemi abil. See tähendab, et AC=2(a(√3)/2)=a(√3).
- Kolmnurgad ABC, CDE ja AEF on kahes küljes ja nendevahelises nurgas võrdsed ning sellest järeldub, et küljed AC, CE ja EA on võrdsed.
Üksteisega lõikuvad kolmnurgad moodustavad uue kuusnurga ja see on samuti korrapärane. Seda tõestatakse lihtsalt:
Seega vastab kujund tavalise kuusnurga omadustele – sellel on kuus võrdset külge ja nurka. Kolmnurkade võrdsusest tippudes on lihtne tuletada uue kuusnurga külje pikkust:
d=a(√3)/3
See on ka selle ümber kirjeldatud ringi raadius. Sisestatud raadius on poole väiksem suure kuusnurga külje suurusest, mis tõestati kolmnurga ABC arvessevõtmisel. Selle kõrgus on täpselt pool küljest, seega on teine pool väikesesse kuusnurka kirjutatud ringi raadius:
r₂=a/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Selgub, et Taaveti tähe sees oleva kuusnurga pindala on kolm korda väiksem kui suurel, kuhu täht on kirjutatud.
Teooriast praktikasse
Kuusnurga omadusi kasutatakse väga aktiivselt nii looduses kui ka erinevates inimtegevuse valdkondades. Esiteks puudutab see polte ja mutreid - esimese ja teise pead pole midagi muud kui tavaline kuusnurk, kui te ei arvesta faasidega. Suurus mutrivõtmed vastab sisse kirjutatud ringi läbimõõdule - see tähendab vastaskülgede vahelisele kaugusele.
Oma kasutuse on leidnud ka kuusnurksed plaadid. See on palju vähem levinud kui nelinurkne, kuid seda on mugavam laduda: ühes punktis kohtuvad kolm plaati, mitte neli. Kompositsioonid võivad olla väga huvitavad:
Samuti toodetakse betoonplaate sillutiseks.
Kuusnurkade levimust looduses selgitatakse lihtsalt. Seega on kõige lihtsam ringid ja pallid tasapinnale tihedalt sobitada, kui need on sama läbimõõduga. Tänu sellele on kärgedel selline kuju.
